安徽省阜阳地区2020年中考数学一模试卷

试卷更新日期：2020-06-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数 $a 、 b 、 c$ 在数轴上的对应点的位置如图所示，则正确的结论是（　　）

A、 $- a > c$ B、 $a > b$ C、 $a b > 0$ D、 $a > - 3$

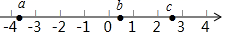查看试题解析
2. 一种细胞的直径约为0.000052米，将0.000052用科学记数法表示为（　　）

A、 $5.2 \times 10^{5}$ B、 $5.2 \times 10^{- 5}$ C、 $5.2 \times 10^{- 4}$ D、 $52 \times 10^{- 6}$

查看试题解析
3. 如图，直线a∥b，直线l与a，b分别交于点A，B，过点A作AC⊥b于点C，若∠1=50°，则∠2的度数为（）

A、130° B、50° C、40° D、25°

查看试题解析
4. 在下列图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 在某次体育测试中，九年级（1）班的15名女生仰卧起坐的成绩如表：

成绩（次∕分钟）

44

45

46

47

48

49

人数（人）

1

1

3

3

5

2

则此次测试成绩的中位数和众数分别是（　　）

A、46，48 B、47，47 C、47，48 D、48，48

查看试题解析
6. 如图，四边形ABCD是⊙O的内接正方形，点P是劣弧弧AB上任意一点（与点B不重合），则∠BPC的度数为（）

A、30° B、45° C、60° D、90°

查看试题解析
7. 如图， $l_{1}$ 反映了某公司的销售收入（单位：元）与销售量（单位：吨）的关系， $l_{2}$ 反映了该公司的销售成本（单位：元）与销售量（单位：吨）的关系，当该公司盈利（收入大于成本）时，销售量应为（　　）

A、大于4吨 B、等于5吨 C、小于5吨 D、大于5吨

查看试题解析
8. 如图，某河的同侧有 $A$ ， $B$ 两个工厂，它们垂直于河边的小路的长度分别为 $A C = 2 k m$ ， $B D = 3 k m$ ，这两条小路相距 $5 k m$ ．现要在河边建立一个抽水站，把水送到 $A$ ， $B$ 两个工厂去，若使供水管最短，抽水站应建立的位置为（　　）

A、距 $C$ 点 $1 k m$ 处 B、距 $C$ 点 $2 k m$ 处 C、距 $C$ 点 $3 k m$ 处 D、 $C D$ 的中点处

查看试题解析
9. 如图是北京2017年3月1日﹣7日的 $P M 2.5$ 浓度（单位： $μ g / m^{3}$ ）和空气质量指数（简称 $A Q I$ ）的统计图，当 $A Q I$ 不大于50时称空气质量为“优”，由统计图得到下列说法：

①3月4日的 $P M 2.5$ 浓度最高

②这七天的 $P M 2.5$ 浓度的平均数是 $30 μ g / m^{3}$

③这七天中有5天的空气质量为“优”

④空气质量指数 $A Q I$ 与 $P M 2.5$ 浓度有关

其中说法正确的是（　　）

A、②④ B、①③④ C、①③ D、①④

查看试题解析
10. 如图1，在矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，动点 $P$ 从点 $B$ 出发，在线段 $B C$ 上匀速运动，到达点 $C$ 时停止．设点 $P$ 运动的路程为 $x$ ，线段 $O P$ 的长为 $y$ ，如果 $y$ 与 $x$ 的函数图象如图2所示，则矩形 $A B C D$ 的面积是（　　）

A、20 B、24 C、48 D、60

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{x + 2}$ 有意义，则x的取值范围为．

查看试题解析
12. 分解因式： $a^{2} b - 4 a b + 4 b =$ ．

查看试题解析
13. 如图，△ABC是⊙O的内接正三角形，图中阴影部分的面积是12π，则⊙O的半径为.

查看试题解析
14. 关于x的一元二次方程ax²+2x+c＝0（a≠0）有两个相等的实数根，写出一组满足条件的实数a，c的值：a＝， c＝.

查看试题解析
15. 下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程．
已知：线段 $a$ ．求作：等腰 $Δ A B C$ ，使 $A B = A C ， B C = a$ ， $B C$ 边上的高为 $2 a$ ．作法：如图，（1）作线段 $B C = a$ ；（2）作线段 $B C$ 的垂直平分线 $D E$ 交 $B C$ 于点 $F$ ；（3）在射线 $F D$ 上顺次截取线段 $F G = G A = a$ ，连接 $A B ， A C$ ．所以 $Δ A B C$ 即为所求作的等腰三角形．

请回答：得到 $Δ A B C$ 是等腰三角形的依据是：

①：

② ．

查看试题解析

16. 某林业部门统计某种树苗在本地区一定条件下的移植成活率，结果如表：

移植的棵数 $n$	300	700	1000	5000	15000
成活的棵数 $m$	280	622	912	4475	13545
成活的频率 $\frac{m}{n}$	0.933	0.889	0.912	0.895	0.903

根据表中的数据，估计这种树苗移植成活的概率为（精确到0.1）；如果该地区计划成活4.5万棵幼树，那么需要移植这种幼树大约万棵．

查看试题解析

三、解答题

17. 计算： ${(π - 2017)}^{0} + 6 \cos 45^{0} + \sqrt[3]{8} - | - 3 \sqrt{2} |$ ．

查看试题解析
18. 解不等式 $\frac{2 x + 1}{3} - \frac{5 x - 1}{2} \geq - 1$ ，并把它的解集在数轴上表示出来．

查看试题解析
19. 如图，在△ABC中，CD=CA，CE⊥AD于点E，BF⊥AD于点F．求证：∠ACE=∠DBF．

查看试题解析
20. 已知 $x^{2} - 10 x y + 25 y^{2} = 0$ ，且 $x y \neq 0$ ，求代数式 $\frac{3 x}{x + 3 y} - \frac{2 x^{2}}{x^{2} - 9 y^{2}} \div \frac{x}{x - 3 y}$ 的值．

查看试题解析
21. 列方程或方程组解应用题：
某校的软笔书法社团购进一批宣纸，用720元购进的用于创作的宣纸与用120元购进的用于练习的宣纸的数量相同，已知用于创作的宣纸的单价比用于练习的宣纸的单价多1元，求用于练习的宣纸的单价是多少元∕张？

查看试题解析
22. 如图，四边形ABCD是矩形，点E在AD边上，点F在AD的延长线上，且BE=CF．

(1)、求证：四边形EBCF是平行四边形．

(2)、若∠BEC=90°，∠ABE=30°，AB= $\sqrt{3}$ ，求ED的长．

查看试题解析
23. 如图，在平面直角坐标系xOy中，直线 $y = k x + 3 (k \neq 0)$ 与x轴交于点A，与双曲线 $y = \frac{m}{x} (m \neq 0)$ 的一个交点为B（－1，4）.

(1)、求直线与双曲线的表达式；

(2)、过点B作BC⊥x轴于点C，若点P在双曲线 $y = \frac{m}{x}$ 上，且△PAC的面积为4，求点P的坐标.

查看试题解析
24. 绿色出行是对环境影响最小的出行方式，“共享单车”已成为北京的一道靓丽的风景线．某社会实践活动小
组为了了解“共享单车”的使用情况，对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查，

以下是根据调查结果绘制的统计图的一部分：

请根据以上信息解答下列问题：

(1)、3月7日使用“共享单车”的教师人数为人，并请补全条形统计图；

(2)、不同品牌的“共享单车”各具特色，社会实践活动小组针对有过使用“共享单车”经历的教师做了进一步调查，每位教师都按要求选择了一种自己喜欢的“共享单车”，统计结果如图，其中喜欢 $m o b i k e$ 的教师有36人，求喜欢 $o f o$ 的教师的人数．

查看试题解析
25. 如图，AB为⊙O的直径，弦BC，DE相交于点F，且DE⊥AB于点G，过点C作⊙O的切线交DE的延长线于点H．

(1)、求证：HC=HF；

(2)、若⊙O的半径为5，点F是BC的中点，tan∠HCF=m，写出求线段BC长的思路．

查看试题解析

26. 已知y是x的函数，如表是y与x的几组对应值．

$x$	…	﹣5	﹣4	﹣3	﹣2	0	1	2	3	4	5	…
$y$	…	1.969	1.938	1.875	1.75	1	0	﹣2	﹣1.5	0	2.5	…

小明根据学习函数的经验，利用上述表格所反映出的 $y$ 与 $x$ 之间的变化规律，对该函数的图象与性质进行了探究．

下面是小明的探究过程，请补充完整：

(1)、如图，在平面直角坐标系

x O y

中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；

(2)、根据画出的函数图象，写出：

① $x = - 1$ 对应的函数值 $y$ 约为；

②该函数的一条性质：．

查看试题解析

27. 在平面直角坐标系 $x O y$ 中，抛物线 $C_{1} ： y = x^{2} + b x + c$ 与 $x$ 轴交于点 $A ， B$ （点 $A$ 在点 $B$ 的左侧），对称轴与 $x$ 轴交于点（3，0），且 $A B = 4$ ．

(1)、求抛物线 $C_{1}$ 的表达式及顶点坐标；

(2)、将抛物线 $C_{1}$ 平移，得到的新抛物线 $C_{2}$ 的顶点为（0，﹣1），抛物线 $C_{1}$ 的对称轴与两条抛物线 $C_{1}$ ， $C_{2}$ 围成的封闭图形为 $M$ ．直线 $l ： y = k x + m (k \neq 0)$ 经过点 $B$ ．若直线 $l$ 与图形 $M$ 有公共点，求 $k$ 的取值范围．

查看试题解析
28. 已知在 $R t Δ B A C$ 中， $∠ B A C = 90^{0}$ ， $A B = A C$ ，点 $D$ 为射线 $B C$ 上一点（与点 $B$ 不重合），过点 $C$ 作 $C E ⊥ B C$ 于点 $C$ ，且 $C E = B D$ （点 $E$ 与点 $A$ 在射线 $B C$ 同侧），连接 $A D$ ， $E D$ ．

(1)、如图1，当点 $D$ 在线段 $B C$ 上时，请直接写出 $∠ A D E$ 的度数．

(2)、当点 $D$ 在线段 $B C$ 的延长线上时，依题意在图2中补全图形并判断（1）中结论是否成立？若成立，请证明；若不成立，请说明理由．

(3)、在（1）的条件下， $E D$ 与 $A C$ 相交于点 $P$ ，若 $A B = 2$ ，直接写出 $C P$ 的最大值．

查看试题解析
29. 在平面直角坐标系 $x O y$ 中，点 $P$ 的坐标为 $(a ， b)$ ，点 $P$ 的变换点 $P^{'}$ 的坐标定义如下：
当 $a > b$ 时，点 $P^{'}$ 的坐标为 $(- a ， b)$ ；当 $a \leq b$ 时，点 $P^{'}$ 的坐标为 $(- b ， a)$ ．

(1)、点 $A (3 ， 1)$ 的变换点 $A^{'}$ 的坐标是；点 $B (- 4 ， 2)$ 的变换点为 $B^{'}$ ，连接 $O B ， O B^{'}$ ，则 $∠ B O B^{'} =$ °；

(2)、已知抛物线 $y = - {(x + 2)}^{2} + m$ 与 $x$ 轴交于点 $C$ ， $D$ （点 $C$ 在点 $D$ 的左侧），顶点为 $E$ ．点 $P$ 在抛物线 $y = - {(x + 2)}^{2} + m$ 上，点 $P$ 的变换点为 $P^{'}$ ．若点 $P^{'}$ 恰好在抛物线的对称轴上，且四边形 $E C P^{'} D$ 是菱形，求 $m$ 的值；

(3)、若点 $F$ 是函数 $y = - 2 x - 6 (- 4 \leq x \leq - 2)$ 图象上的一点，点 $F$ 的变换点为 $F^{'}$ ，连接 $F F^{'}$ ，以 $F F^{'}$ 为直径作 $⊙ M$ ， $⊙ M$ 的半径为 $r$ ，请直接写出 $r$ 的取值范围．

查看试题解析

成绩（次∕分钟）	44	45	46	47	48	49
人数（人）	1	1	3	3	5	2