安徽省亳州市2020年中考数学二模试卷

试卷更新日期：2020-06-10 类型：中考模拟

进入出卷网下载

一、单选题

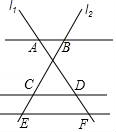
1. 下列图形中，一定相似的是（　　）

A、两个正方形 B、两个菱形 C、两个直角三角形 D、两个等腰三角形

查看试题解析
2. 如图，已知AB∥CD∥EF，它们依次交直线l₁、l₂于点A、D、F和点B、C、E，如果AD：DF＝3：1，BE＝10，那么CE等于（）

A、 $\frac{10}{3}$ B、 $\frac{20}{3}$ C、 $\frac{5}{2}$ D、 $\frac{15}{2}$

查看试题解析
3. 在Rt△ABC中，∠C＝90°，如果∠A＝α，BC＝a，那么AC等于（）

A、a•tanα B、a•cotα C、a•sinα D、a•cosα

查看试题解析
4. 下列判断错误的是（　　）

A、0• $\overset{⇀}{a} = \overset{⇀}{0}$ B、如果+2 $\vec{c}$ ， $\vec{a}$ - $\vec{b}$ =3 $\vec{c}$ ，其中 $\vec{c} \neq \vec{0}$ ，那么 $\vec{a}$ ∥ $\vec{b}$ C、设 $\vec{e}$ 为单位向量，那么| $\vec{e}$ |=1 D、如果| $\vec{a}$ |=2| $\vec{b}$ |，那么 $\vec{a}$ =2 $\vec{b}$ 或 $\vec{a}$ =-2 $\vec{b}$

查看试题解析
5. 如图，已知△ABC，D、E分别在边AB、AC上，下列条件中，不能确定△ADE∽△ACB的是（　　）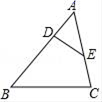

A、∠AED＝∠B B、∠BDE+∠C＝180° C、AD•BC＝AC•DE D、AD•AB＝AE•AC

查看试题解析
6. 已知二次函数y＝ax²+bx+c的图象如图所示，那么下列结论中正确的是（　）

A、ac＞0 B、b＞0 C、a+c＜0 D、a+b+c＝0

查看试题解析

二、填空题

7. 如果 $\frac{x}{x + y}$ ＝ $\frac{2}{5}$ ，那么 $\frac{x}{y}$ ＝．

查看试题解析
8. 计算：3（ $\vec{a}$ -2 $\vec{b}$ ）﹣2（ $\vec{a}$ -3 $\vec{b}$ ）＝．

查看试题解析
9. 两个相似三角形的相似比为1：3，则它们周长的比为．

查看试题解析
10. 二次函数 $y = x^{2} - 4 x - 1$ 的图像的顶点坐标是．

查看试题解析
11. 抛物线y＝﹣x²+mx﹣3m的对称轴是直线x＝1，那么m＝．

查看试题解析
12. 抛物线y＝x²﹣2在y轴右侧的部分是．（填“上升”或“下降”）

查看试题解析
13. 如果α是锐角，且sinα＝cos20°，那么α＝度．

查看试题解析
14. 如图，某水库大坝的橫断面是梯形ABCD，坝高为15米，迎水坡CD的坡度为1：2.4，那么该水库迎水坡CD的长度为米．

查看试题解析
15. 如图，在边长相同的小正方形组成的网格中，点A、B、C都在这些小正方形的顶点上，则tan∠ABC的值为．

查看试题解析
16. 在△ABC中，AB＝AC，高AH与中线BD相交于点E，如果BC＝2，BD＝3，那么AE＝．

查看试题解析
17. 如图，在Rt△ABC中，∠ACB＝90°，AC＝1，tan∠CAB＝2，将△ABC绕点A旋转后，点B落在AC的延长线上的点D，点C落在点E，DE与直线BC相交于点F，那么CF＝．

查看试题解析
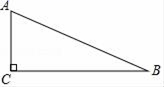18. 对于封闭的平面图形，如果图形上或图形内的点S到图形上的任意一点P之间的线段都在图形内或图形上，那么这样的点S称为“亮点”．如图，对于封闭图形ABCDE，S₁是“亮点”，S₂不是“亮点”，如果AB∥DE，AE∥DC，AB＝2，AE＝1，∠B＝∠C＝60°，那么该图形中所有“亮点”组成的图形的面积为．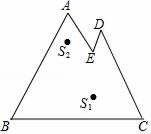

查看试题解析

三、解答题

19. 计算：（sin30°）^﹣¹+|1﹣cot30°|+ $\sqrt{3}$ tan30°﹣ $\frac{1}{\cos^{2} 45^{0}}$ ．

查看试题解析
20. 如图，在平行四边形ABCD中，点E在边BC上，CE＝2BE，AC、DE相交于点F．

(1)、求DF：EF的值；

(2)、如果 $\vec{C B}$ = $\vec{a}$ ， $\vec{C B}$ = $\vec{b}$ ，试用 $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{E F}$ ．

查看试题解析
21. 如图，在△ABC中，点D、E分别在边AB、AC上，AE²＝AD•AB，∠ABE＝∠ACB．

(1)、求证：DE∥BC；

(2)、如果S_△_ADE：S_四边形_DBCE＝1：8，求S_△_ADE：S_△_BDE的值．

查看试题解析
22. 如图，在港口A的南偏东37°方向的海面上，有一巡逻艇B，A、B相距20海里，这时在巡逻艇的正北方向及港口A的北偏东67°方向上，有一渔船C发生故障.得知这一情况后，巡逻艇以25海里/小时的速度前往救援，问巡逻艇能否在1小时内到达渔船C处？
(参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin67°≈ $\frac{12}{13}$ ，cos67°≈ $\frac{5}{13}$ tan67°≈ $\frac{12}{5}$ )

查看试题解析
23. 已知：如图，在△ABC中，点D、E分别在边BC、AC上，点F在DE的延长线上，AD＝AF，AE•CE＝DE•EF．

(1)、求证：△ADE∽△ACD；

(2)、如果AE•BD＝EF•AF，求证：AB＝AC．

查看试题解析
24. 在平面直角坐标系xOy中，将抛物线y＝﹣x²平移后经过点A（﹣1，0）、B（4，0），且平移后的抛物线与y轴交于点C（如图）．

(1)、求平移后的抛物线的表达式；

(2)、如果点D在线段CB上，且CD＝ $\sqrt{2}$ ，求∠CAD的正弦值；

(3)、点E在y轴上且位于点C的上方，点P在直线BC上，点Q在平移后的抛物线上，如果四边形ECPQ是菱形，求点Q的坐标．

查看试题解析
25. 如图，在梯形ABCD中，AD∥BC，BC＝18，DB＝DC＝15，点E、F分别在线段BD、CD上，DE＝DF＝5．AE的延长线交边BC于点G，AF交BD于点N、其延长线交BC的延长线于点H．

(1)、求证：BG＝CH；

(2)、设AD＝x，△ADN的面积为y，求y关于x的函数解析式，并写出它的定义域；

(3)、联结FG，当△HFG与△ADN相似时，求AD的长．

查看试题解析