安徽省合肥市瑶海区2020年中考数学一模试卷

试卷更新日期：2020-06-10 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的相反数是（）

A、3 B、 $\frac{1}{3}$ C、 $- 3$ D、 $- \frac{1}{3}$

查看试题解析
2. 如图是由两个小正方体和一个圆锥体组成的立体图形，其主视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 据新安晚报报道，2019年安徽省全年进出口总额为687.3亿美元，其中687.3亿用科学记数法表示为（）

A、6.873×10⁸ B、6.873×10¹⁰ C、6.873×10¹¹ D、687.3×10⁸

查看试题解析
4. 估计 $\sqrt{27} - \sqrt{3}$ 的运算结果在（）

A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间

查看试题解析
5. 计算 $\frac{x - 1}{x^{2} - 1} + \frac{x}{x + 1}$ 的结果为（）

A、-1 B、1 C、 $\frac{1}{x + 1}$ D、 $\frac{1}{x - 1}$

查看试题解析
6. 2019年第一季度，安徽省某企业生产总值比2018年同期增长14%，2020年第一季度受新冠肺炎疫情影响，生产总值比2019年同期减少了9%，设2019年和2020年第一季度生产总值平均增长率为x，则可列方程为（）

A、2x=14%-9% B、（1+x）²=1+14%-9% C、（1+x）²=（1+14%）（1-9%） D、1+2x=（1+14%）（1-9%）

查看试题解析
7. 如图，D、E分别是△ABC的边AB、AC的中点，H、G是边BC上的点，且HG= $\frac{1}{2}$ BC，S_△_ABC =12，则图中阴影部分的面积为（）

A、6 B、4 C、3 D、2

查看试题解析
8. 校团委组织开展“医助武汉捐款”活动，小慧所在的九年级（1）班共40名同学进行了捐款，已知该班同学捐款的平均金额为10元，二小慧捐款11元，下列说法错误的是（）

A、10元是该班同学捐款金额的平均水平 B、班上比小慧捐款金额多的人数可能超过20人 C、班上捐款金额的中位数一定是10元 D、班上捐款金额数据的众数不一定是10元

查看试题解析
9. 小明和小亮两人在长为50m的直道AB（A、B为直道两端点）上进行匀速往返跑训练，两人同时从A点起跑，到达B点后，立即转身跑向A点，到达A点后，又立即转身跑向B点……若小明跑步速度为5m/s，小亮跑步速度为4m/s，则起跑后60s内，两人相遇的次数为（）

A、3 B、4 C、5 D、6

查看试题解析
10. 如图所示，已知矩形ABCD，AB=4，AD=3，点E为边DC上不与端点重合的一个动点，连接BE，将BCE沿BE翻折得到BEF，连接AF并延长交CD于点G，则线段CG的最大值是（）

A、1 B、1.5 C、4- $\sqrt{5}$ D、4- $\sqrt{7}$

查看试题解析

二、填空题

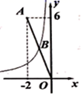
11. 因式分解：x³﹣4xy²= ．

查看试题解析
12. 如图，在平面直角坐标系中，点A的坐标为（-2，6），反比例函数 $y = \frac{k}{x}$ （x＜0）线段OA的中点B，则k的值为

查看试题解析
13. 如图，正方形 $A B C D$ 的四个顶点分别在扇形 $O E F$ 的半径 $O E$ ， $O F$ 和 $\overset{⌢}{E F}$ 上，且点 $A$ 是线段 $O B$ 的中点，若 $\overset{⌢}{E F}$ 的长为 $\sqrt{5} π$ ，则 $O D$ 长为．

查看试题解析
14. 抛物线y=x²+2ax-3与x轴交于A、B（1，0）两点（点A在点B的左侧），与y轴交于点C，将抛物线沿y轴平移m（m＞0）个单位，当平移后的抛物线与线段OA有且只有一个交点时，则m的取值范围是

查看试题解析

三、解答题

15. 计算： ${(- 2020)}^{0} + | - \sqrt{2} | \cdot \sin 45^{°} - {(\frac{1}{2})}^{- 2}$

查看试题解析
16. 解不等式组： ${\begin{array}{l} \frac{x + 2}{3} < 2 \\ x - 4 \leq 3 x - 4 \end{array}$

查看试题解析
17. 如图所示，方格纸中的每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上．

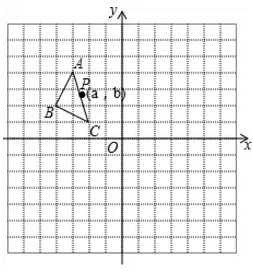(1)、将△ABC向下平移5个单位再向右平移1个单位后得到对应的△A₁B₁C₁ ，画出△A₁B₁C₁；

(2)、画出△A₁B₁C₁关于y轴对称的△A₂B₂C₂；

(3)、P（a，b）是△ABC的边AC上一点，请直接写出经过两次变换后在△A₂B₂C₂中对应的点P₂的坐标．

查看试题解析
18. 观察下列等式的规律：第1个等式： $\frac{1}{1} - \frac{1}{3} = \frac{2}{2^{2} - 1}$ ；第2个等式： $\frac{1}{3} - \frac{1}{5} = \frac{2}{4^{2} - 1}$ ；第3个等式： $\frac{1}{5} - \frac{1}{7} = \frac{2}{6^{2} - 1}$ ；第4个等式： $\frac{1}{7} - \frac{1}{9} = \frac{2}{8^{2} - 1}$ ；第5个等式： $\frac{1}{9} - \frac{1}{11} = \frac{2}{10^{2} - 1}$ ；…….；按照以上规律，解决下列问题：

(1)、直接写出第6个等式：

(2)、请写出你猜想的第n个等式（用含n的代数式表示），并证明．

查看试题解析
19. 下表是小安填写的数学实践活动报告的部分内容

题目

测量铁塔顶端到地面的高度

测量目标示意图

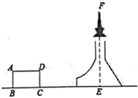
相关数据

CD=20m，ɑ=45°，β=52°

求铁塔的高度FE（结果精确到1米）（参考数据：sin52°≈0.79， cos52°≈0.62，tan52°≈1.28）

查看试题解析
20. 如图，在四边形ABCD中， $AD / / BC$ ， $∠ ABC = 90^{\circ}$ ，点P是边AB上一点.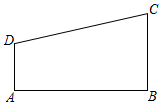

(1)、若 $△ PAD$ ∽ $△ CBP$ ，请利用没有刻度的直尺和圆规，画出满足条件的所有点P.

(2)、在（1）的条件下，若 $AB = 8$ ， $AD = 3$ ， $BC = 4$ ，则AP的长是．

查看试题解析
21. 为调查某市市民上班时最常用的交通工具的情况，随机抽取了部分市民进行调查，要求被调查者从“ $A$ ：自行车， $B$ ：家庭汽车， $C$ ：公交车， $D$ ：电动车， $E$ ：其他”五个选项中选择最常用的一项，将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图，请结合统计图回答下列问题．

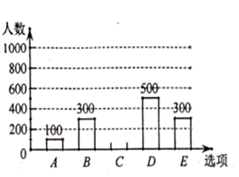(1)、本次调查中，一共调查了名市民；扇形统计图中， $A$ 项对应的扇形圆心角是 $^{°}$ .

(2)、补全条形统计图.

(3)、若甲上班时从A、B、C三种交通工具中随机选择一种，乙上班时从B、C、D三种交通工具中随机选择一种，请用列表法或画树状图的方法，求出甲、乙两人都不选 $B$ 种交通工具上班的概率．

查看试题解析
22. 如图，二次函数y=-x²+（n-1）x+3的图像与y轴交于点A，与x轴的负半轴交于点B（-2，0）

(1)、求二次函数的解析式；

(2)、点P是这个二次函数图象在第二象限内的一线，过点P作y轴的垂线与线段AB交于点C，求线段PC长度的最大值．

查看试题解析
23. 如图1，正方形ABCD中，点E是BC的中点，过点B作BG⊥AE于点G，过点C作CF垂直BG的延长线于点H，交AD于点F

(1)、求证：△ABG≌△BCH；

(2)、如图2，连接AH，连接EH并延长交CD于点I.
求证：① AB²=AE·BH；②求 $\frac{D I}{I C}$ 的值；

查看试题解析

题目	测量铁塔顶端到地面的高度
测量目标示意图
相关数据	CD=20m，ɑ=45°，β=52°