云南省昆明市2020年数学中考一模试卷
试卷更新日期:2020-06-09 类型:中考模拟
一、填空题
-
1. 规定: 表示向右移动 记作 ,则 表示向左移动 记作:2. 中新网昆明2月26日电: 1月24日至2月25日,云南铁路累计抢运支援湖北疫情防控保障物资 批,约 吨. 这个数用科学记数法表示为3. 代数式 有意义时,x应满足的条件是.4. 如图所示,直线 ,直线 分别与 相交于点 小宇同学利用尺规按以下步骤作图:①以点 为圆心,以任意长为半径作弧交于 点 ,交 于点 ;②分别以 为圆心,以大于 长为半径作弧,两弧在 内交于点 ;③作射线 交 于点 .若 ,则 的度数为
 5. 如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为 .
5. 如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为 .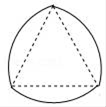 6. 在直角三角形ABC中,若2AB=AC,则cosC=.
6. 在直角三角形ABC中,若2AB=AC,则cosC=.二、选择题
-
7. 面积为4的正方形的边长是( )A、4的平方根 B、4的算术平方根 C、4开平方的结果 D、4的立方根8. 某几何体的三视图如图所示,则该几何体可能是( )
 A、长方体 B、正方体 C、球 D、圆柱9. 下列运算正确的是( )A、 B、 C、 D、10. 某同学要统计本校图书馆最受学生欢迎的图书种类,以下是排乱的统计步骤:
A、长方体 B、正方体 C、球 D、圆柱9. 下列运算正确的是( )A、 B、 C、 D、10. 某同学要统计本校图书馆最受学生欢迎的图书种类,以下是排乱的统计步骤:①从扇形图中分析出最受学生欢迎的种类
②去图书馆收集学生借阅图书的记录
③绘制扇形图来表示各个种类所占的百分比
④整理借阅图书记录并绘制频数分布表
正确统计步骤的顺序是( )
A、②→③→①→④ B、③→④→①→② C、①→②→④→③ D、②→④→③→①11. 不等式组 的解集在数轴上表示为( )A、 B、
B、 C、
C、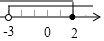 D、
D、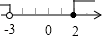 12. 能说明命题“关于 的方程 一定有实数根”是假命题的反例为( )A、 B、 C、 D、13. 一道来自课本的习题:
12. 能说明命题“关于 的方程 一定有实数根”是假命题的反例为( )A、 B、 C、 D、13. 一道来自课本的习题:从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min,甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数x,y,已经列出一个方程 ,则另一个方程正确的是( )
A、 B、 C、 D、14. 如图所示, 中, ,顶点 分别在反比例函数 与 的图象器上,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
15. 化简: ,圆圆的解答如下: ,圆圆的解答正确吗?如果不正确,写出正确的解答,并求出当 时,代数式的值.16. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.
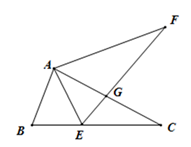 (1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.17. 红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
(1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.17. 红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数
人数
班级
60
70
80
90
100
1班
0
1
6
2
1
2班
1
1
3
1
3班
1
1
4
2
2
分析数据:
平均数
中位数
众数
1班
83
80
80
2班
83
3班
80
80
根据以上信息回答下列问题:
(1)、请直接写出表格中 的值;(2)、比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;(3)、为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?18. 如图,矩形 中,点 在边 上,将 沿 折叠,点 落在 边上的点 处,过点 作 交 于点 ,连接 .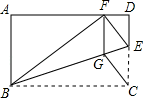 (1)、求证:四边形 是菱形;(2)、若 ,求四边形 的面积.19. 现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。(1)、将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;(2)、小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。20. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?21. 某宾馆有若干间标准房,当标准房的价格为 元时,每天入住的国间数为 间,经市场调查表明,该宾馆每间标准房的价格在 元之间(含 元, 元)浮动时,每天人住的房间数 (间)与每间标准房的价格 (元)的数据如下表:
(1)、求证:四边形 是菱形;(2)、若 ,求四边形 的面积.19. 现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。(1)、将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;(2)、小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。20. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?21. 某宾馆有若干间标准房,当标准房的价格为 元时,每天入住的国间数为 间,经市场调查表明,该宾馆每间标准房的价格在 元之间(含 元, 元)浮动时,每天人住的房间数 (间)与每间标准房的价格 (元)的数据如下表:(元)
……
190
200
210
220
……
(元)
……
65
60
55
50
……
 (1)、根据所给数据在坐标系中描出相应的点,并画出图象.(2)、猜想(1)中的图象是什么函数的图象,求 关于 的函数表达式,并写出自变量 的取值范围.(3)、设客房的日营业额为W (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?22. 如图所示,在平面内,给定不在同一直线上的点 , , ,射线 是 的平分线,点 到点 , , 的距离均等于 ( 为常数),到点 的距离等于 的所有点组成图形 ,图形 交射线 于点 ,连接 , .
(1)、根据所给数据在坐标系中描出相应的点,并画出图象.(2)、猜想(1)中的图象是什么函数的图象,求 关于 的函数表达式,并写出自变量 的取值范围.(3)、设客房的日营业额为W (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?22. 如图所示,在平面内,给定不在同一直线上的点 , , ,射线 是 的平分线,点 到点 , , 的距离均等于 ( 为常数),到点 的距离等于 的所有点组成图形 ,图形 交射线 于点 ,连接 , .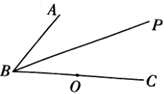 (1)、求证: ;(2)、过点 作直线 的垂线 ,垂足为 ,作 于点 ,延长 交图形 于点 ,连接 .若 ,求直线 与图形 的公共点个数.23. 如图,抛物线 过点 ,且与直线 交于B、C两点,点B的坐标为 .
(1)、求证: ;(2)、过点 作直线 的垂线 ,垂足为 ,作 于点 ,延长 交图形 于点 ,连接 .若 ,求直线 与图形 的公共点个数.23. 如图,抛物线 过点 ,且与直线 交于B、C两点,点B的坐标为 .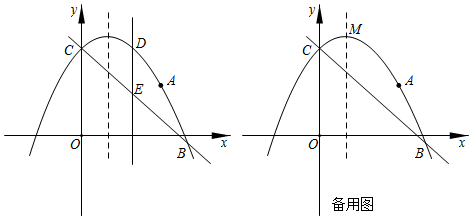 (1)、求抛物线的解析式;(2)、点D为抛物线上位于直线 上方的一点,过点D作 轴交直线 于点E , 点P为对称轴上一动点,当线段 的长度最大时,求 的最小值;(3)、设点M为抛物线的顶点,在y轴上是否存在点Q , 使 ?若存在,求点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点D为抛物线上位于直线 上方的一点,过点D作 轴交直线 于点E , 点P为对称轴上一动点,当线段 的长度最大时,求 的最小值;(3)、设点M为抛物线的顶点,在y轴上是否存在点Q , 使 ?若存在,求点Q的坐标;若不存在,请说明理由.