云南省红河州蒙自市2020年数学中考一模试卷

试卷更新日期：2020-06-09 类型：中考模拟

进入出卷网下载

一、填空题

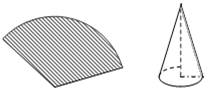
1. - 2020的倒数是

查看试题解析
2. 截至2020年3月11日09时，全国累计报告确诊COVID-19病例80955例，累计死亡病例3162例，累计治愈出院61567例. 将数据80955用科学记数法表示为.

查看试题解析
3. 分解因式：x²﹣9x= ．

查看试题解析
4. 如图，用圆心角为120°，半径为6cm的扇形纸片卷成一个圆锥形无底纸帽，则这个纸帽的高是cm ．

查看试题解析
5. 在△AOC中，OB交AC于点D，量角器的摆放如图所示，则∠CDO的度数为 .

查看试题解析
6. 如图，将正整数的算术平方根按如图所示的规律排列下去.若用有序实数对（m，n）表示第m排，从左到右第n个数，如（4，3）表示实数3，则（8，6）表示的实数是.

查看试题解析

二、选择题

7. 剪纸是我国传统的民间艺术，下列剪纸作品中既不是轴对称图形，也不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 某篮球运动员在连续7场比赛中的得分(单位：分)依次为21，16，17，23，20，20，23，则这组数据的平均数与中位数分别是（）

A、20分，17分 B、20分，22分 C、20分，19分 D、20分，20分

查看试题解析
9. 下列运算正确的是（）

A、 ${(a - 3)}^{2} = a^{2} - 9$ B、 $a^{2} • a^{4} = a^{8}$ C、 $\sqrt{9} = \pm 3$ D、 $\sqrt[3]{- 8} = - 2$

查看试题解析
10. 若 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
11. 关于 $x$ 的方程 $k x^{2} + 3 x - 1 = 0$ 有实数根，则k的取值范围是（）

A、 $k \leq - \frac{9}{4}$ B、 $k \leq - \frac{9}{4}$ 且 $k \neq 0$ C、 $k \geq - \frac{9}{4}$ D、 $k \geq - \frac{9}{4}$ 且 $k \neq 0$

查看试题解析
12. 如图，已知A为反比例函数 $y = \frac{k}{x}$ （ $x$ <0）的图像上一点，过点A作AB⊥ $y$ 轴，垂足为B.若△OAB的面积为2，则k的值为（）

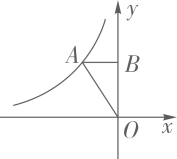A、2 B、-2 C、4 D、-4

查看试题解析
13. “绿水青山就是金山银山”．某工程队承接了60万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了25%，结果提前30天完成了这一任务．设实际工作时每天绿化的面积为x万平方米，则下面所列方程中正确的是（）

A、 $\frac{60}{x} - \frac{60}{(1 + 25 %) x} = 30$ B、 $\frac{60}{(1 + 25 %) x} - \frac{60}{x} = 30$ C、 $\frac{60 \times (1 + 25 %)}{x} - \frac{60}{x} = 30$ D、 $\frac{60}{x} - \frac{60 \times (1 + 25 %)}{x} = 30$

查看试题解析
14. 如图，已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O.下列结论：①∠DOC=90°， ②OC=OE， ③tan∠OCD = $\frac{4}{3}$ ，④ $S_{Δ ODC} = S_{四边形 BEOF}$ 中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

三、解答题

15. 计算： ${(- 2020)}^{0} - | - \sqrt{2} | + {(\frac{1}{3})}^{- 1} + 2 \sin 45^{\circ}$ .

查看试题解析
16. 如图，点A、E、B、D在同一条直线上，AE=BD，AC=DF，AC∥DF.求证：BC∥EF.

查看试题解析
17. 如图，已知△ABC 的顶点分别为 A（-2，2）、B（-4，5）、C（-5，1）和直线 m （直线 m 上各点的横坐标都为 1）.

①作出△ABC 关于 $x$ 轴对称的图形△A₁B₁C₁ ，并写出点 A₁ 的坐标；

②作出点 C关于直线 m 对称的点C₂ ，并写出点C₂ 的坐标；

③在 $x$ 轴上找一点P，使 PA+PC的值最小，请直接写出点P的坐标.

查看试题解析
18. 随着智能手机的普及率越来越高以及移动支付的快捷高效性，中国移动支付在世界处于领先水平.为了解人们平时最喜欢用哪种移动支付方式，因此在某步行街对行人进行随机抽样调查，以下是根据调查结果分别整理的不完整的统计表和统计图.

移动支付方式

支付宝

微信

其他

人数/人

200

75

请你根据上述统计表和统计图提供的信息.完成下列问题：

(1)、在此次调查中，使用支付宝支付的人数；

(2)、求表示微信支付的扇形所对的圆心角度数；

(3)、某天该步行街人流量为10万人，其中30%的人购物并选择移动支付，请你依据此次调查获得的信息估计一下当天使用微信支付的人数.

查看试题解析
19. 在歌唱比赛中，一位歌手分别转动如下的两个转盘（每个转盘都被分成3等份）一次，根据指针指向的歌曲名演唱两首曲目.

(1)、转动转盘①时，该转盘指针指向歌曲“3”的概率是；

(2)、若允许该歌手替换他最不擅长的歌曲“3”，即指针指向歌曲“3”时，该歌手就选择自己最擅长的歌曲“1”，求他演唱歌曲“1”和“4”的概率.

查看试题解析
20. 如图，在矩形ABCD中，AB＝16，AD＝12，点E、F分别在边CD、AB上.

(1)、若DE＝BF，求证：四边形AFCE是平行四边形；

(2)、若四边形AFCE是菱形，求菱形AFCE的周长.

查看试题解析
21. 某网店专售一款电动牙刷，其成本为20元/支，销售中发现，该商品每天的销售量y（支）与销售单价x（元/支）之间存在如图所示的关系.

(1)、请求出y与x的函数关系式；

(2)、该款电动牙刷销售单价定为多少元时，每天销售利润最大？最大利润是多少元？

(3)、近期武汉爆发了“新型冠状病毒”疫情，该网店店主决定从每天获得的利润中抽出 200 元捐赠给武汉，为了保证捐款后每天剩余利润不低于550元，如何确定该款电动牙刷的售单价？

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，以CD为直径的⊙O分别交AC，BC于点E，F两点，过点F作FG⊥AB于点G．

(1)、试判断FG与⊙O的位置关系，并说明理由．

(2)、若AC＝3，CD＝2.5，求FG的长．

查看试题解析
23. 如图1，在△ABC中，AB＝AC＝20，tanB＝ $\frac{3}{4}$ ，点D为BC边上的动点（D不与点B，C重合）.以D为顶点作∠ADE＝∠B，射线DE交AC边于点E，过点A作AF⊥AD交射线DE于点F，连接CF.

(1)、求证：△ABD∽△DCE；

(2)、当DE∥AB时（如图2），求AE的长；

(3)、点D在BC边上运动的过程中，是否存在某个位置，使得DF＝CF？若存在，求出此时BD的长；若不存在，请说明理由.

查看试题解析

移动支付方式	支付宝	微信	其他
人数/人		200	75