新疆生产建设兵团2020年数学中考模拟试卷(4月)
试卷更新日期:2020-06-09 类型:中考模拟
一、选择题
-
1. 下面四个数中比﹣4小的是( )A、3 B、2 C、﹣3 D、﹣52. 如图,AB∥EF,设∠C=90°,那么x、y和z的关系是( )
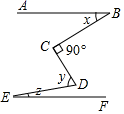 A、y=x+z B、x+y﹣z=90° C、x+y+z=180° D、y+z﹣x=90°3. 下列运算不正确的是( )A、a2•a3=a5 B、(y3)4=y12 C、(﹣2x)3=﹣8x3 D、x3+x3=2x64. 初三(1)班一次体育模拟考试中,10名同学跳绳项目的测试成绩统计如下表:
A、y=x+z B、x+y﹣z=90° C、x+y+z=180° D、y+z﹣x=90°3. 下列运算不正确的是( )A、a2•a3=a5 B、(y3)4=y12 C、(﹣2x)3=﹣8x3 D、x3+x3=2x64. 初三(1)班一次体育模拟考试中,10名同学跳绳项目的测试成绩统计如下表:成绩(个/分钟)
140
160
169
170
177
180
人数
1
1
1
2
3
2
则下列说法错误的是( )
A、平均数是170 B、众数是177 C、中位数是173.5 D、方差是1355. 如图,已知 ,且OC=AC则∠BOC的度数是( )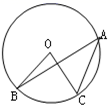 A、70° B、80° C、40° D、60°6. 暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )A、 B、 C、 D、7. 如图,在 中,尺规作图如下:在射线 、 上,分别截取 、 ,使 ;分别以点 和点 为圆心、大于 的长为半径作弧,两弧相交于点 ;作射线 ,连结 、 .下列结论不一定成立的是( )
A、70° B、80° C、40° D、60°6. 暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )A、 B、 C、 D、7. 如图,在 中,尺规作图如下:在射线 、 上,分别截取 、 ,使 ;分别以点 和点 为圆心、大于 的长为半径作弧,两弧相交于点 ;作射线 ,连结 、 .下列结论不一定成立的是( )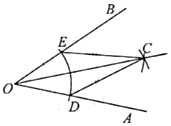 A、 B、 C、 D、8. 已知关于 的方程 有唯一实数解,且反比例函数 的图象在每个象限内 随 的增大而增大,那么反比例函数的关系式为( )A、 B、 C、 D、9. 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2 cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2 , 运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A、 B、 C、 D、8. 已知关于 的方程 有唯一实数解,且反比例函数 的图象在每个象限内 随 的增大而增大,那么反比例函数的关系式为( )A、 B、 C、 D、9. 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2 cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2 , 运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( ) A、
A、 B、
B、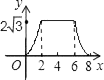 C、
C、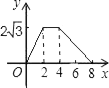 D、
D、
二、填空题
-
10. 要使分式 有意义, 应满足的条件是11. 一个凸多边形的内角和为720°,则这个多边形的边数是12. 若不等式组 解集是 ,则 .13. 在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球不放回,再随机地摸出一个小球,则两次摸出的小球的标号的和为奇数的概率是.
14. 一次函数y=(k−2)x+3−k的图象经过第一、二、三象限,则k的取值范围是.15. 定义新运算若 (n是常数),则 , .若 则 , , .
三、解答题
-
16. 计算:17. 先化简,再求值: ,其中 .18. 泉州市某学校抽样调查学生上学的交通工具,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
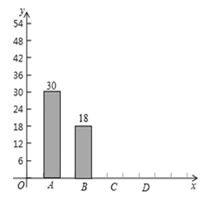
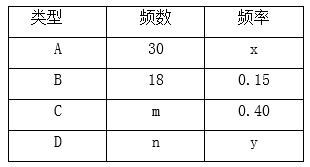 (1)、学生共人,x= , y=;(2)、补全条形统计图;(3)、若该校共有2000人,骑共享单车的有人.19. 已知:如图,AC,BD是▱ABCD的两条对角线,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:EO=FO.
(1)、学生共人,x= , y=;(2)、补全条形统计图;(3)、若该校共有2000人,骑共享单车的有人.19. 已知:如图,AC,BD是▱ABCD的两条对角线,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:EO=FO.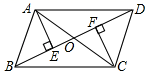 20. 海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
20. 海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由. 21. 如图,点 在 的直径 的延长线上,点 在 上,且AC=CD,∠ACD=120°.
21. 如图,点 在 的直径 的延长线上,点 在 上,且AC=CD,∠ACD=120°. (1)、求证: 是 的切线;
(1)、求证: 是 的切线;
(2)、若 的半径为2,求图中阴影部分的面积.
22. 一条笔直的公路上有甲、乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地设他们同时出发,运动的时间为 (分),与乙地的距离为 (米),图中线段EF,折线 分别表示两人与乙地距离 和运动时间 之间的函数关系图象 (1)、李越骑车的速度为米/分钟;F点的坐标为;
(1)、李越骑车的速度为米/分钟;F点的坐标为;
(2)、求李越从乙地骑往甲地时, 与 之间的函数表达式;
(3)、求王明从甲地到乙地时, 与 之间的函数表达式;
(4)、求李越与王明第二次相遇时 的值.
23. 在平面直角坐标系 中(如图),已知二次函数 (其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC. (1)、求这个二次函数的解析式;(2)、点D是线段AC上的一点,联结BD,如果 ,求tan∠DBC的值;(3)、如果点E在该二次函数图象的对称轴上,当AC平分∠BAE时,求点E的坐标.
(1)、求这个二次函数的解析式;(2)、点D是线段AC上的一点,联结BD,如果 ,求tan∠DBC的值;(3)、如果点E在该二次函数图象的对称轴上,当AC平分∠BAE时,求点E的坐标.