陕西省西安市2020年数学中考四模试卷
试卷更新日期:2020-06-09 类型:中考模拟
一、选择题
-
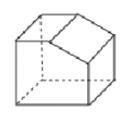
1. ﹣ 的绝对值为( )A、﹣2 B、﹣ C、 D、12. 如图所示的几何体,它的左视图是( )
 A、
A、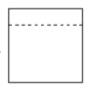 B、
B、 C、
C、 D、
D、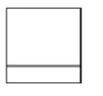 3. 下列各运算中,计算正确的是( )A、a12÷a3=a4 B、(3a2)3=9a6 C、(a﹣b)2=a2﹣ab+b2 D、2a•3a=6a24. 如图,已知AB∥CD,AD=CD,∠1=40°,则∠2的度数为( )
3. 下列各运算中,计算正确的是( )A、a12÷a3=a4 B、(3a2)3=9a6 C、(a﹣b)2=a2﹣ab+b2 D、2a•3a=6a24. 如图,已知AB∥CD,AD=CD,∠1=40°,则∠2的度数为( )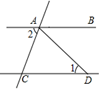 A、60° B、65° C、70° D、75°5. 若正比例函数y=kx的图象上一点(除原点外)到x轴的距离与到y轴的距离之比为3,且y值随着x值的增大而减小,则k的值为( )A、﹣ B、﹣3 C、 D、36. 如图在△ABC中,AC=BC,过点C作CD⊥AB,垂足为点D,过D作DE∥BC交AC于点E,若BD=6,AE=5,则sin∠EDC的值为( )
A、60° B、65° C、70° D、75°5. 若正比例函数y=kx的图象上一点(除原点外)到x轴的距离与到y轴的距离之比为3,且y值随着x值的增大而减小,则k的值为( )A、﹣ B、﹣3 C、 D、36. 如图在△ABC中,AC=BC,过点C作CD⊥AB,垂足为点D,过D作DE∥BC交AC于点E,若BD=6,AE=5,则sin∠EDC的值为( ) A、 B、 C、 D、7. 已知一次函数y=﹣ x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )A、﹣2 B、﹣1 C、1 D、28. 如图,已知矩形ABCD中,BC=2AB,点E在BC边上,连接DE、AE,若EA平分∠BED,则 的值为( )
A、 B、 C、 D、7. 已知一次函数y=﹣ x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )A、﹣2 B、﹣1 C、1 D、28. 如图,已知矩形ABCD中,BC=2AB,点E在BC边上,连接DE、AE,若EA平分∠BED,则 的值为( ) A、 B、 C、 D、9. 如图已知⊙O的内接五边形ABCDE,连接BE、CE,若AB=BC=CE,∠EDC=130°,则∠ABE的度数为( )
A、 B、 C、 D、9. 如图已知⊙O的内接五边形ABCDE,连接BE、CE,若AB=BC=CE,∠EDC=130°,则∠ABE的度数为( ) A、25° B、30° C、35° D、40°10. 已知抛物线y=x2+(2a+1)x+a2﹣a,则抛物线的顶点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
A、25° B、30° C、35° D、40°10. 已知抛物线y=x2+(2a+1)x+a2﹣a,则抛物线的顶点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题
-
11. 不等式 >4﹣x的解集为 .12. 如图,在正六边形ABCDEF中,AC于FB相交于点G,则 值为 .
 13. 若反比例函数y= 的图象与一次函数y=x+k的图象有一个交点为(m,﹣4),则这个反比例函数的表达式为 .14. 如图,已知 ,点 为边 中点,点 在线段 上运动,点 在线段 上运动,连接 ,则 周长的最小值为.
13. 若反比例函数y= 的图象与一次函数y=x+k的图象有一个交点为(m,﹣4),则这个反比例函数的表达式为 .14. 如图,已知 ,点 为边 中点,点 在线段 上运动,点 在线段 上运动,连接 ,则 周长的最小值为.
三、解答题
-
15. 如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
 (1)、求证:DB平分∠ADC;(2)、若EB=10,CD=9,tan∠ABE= ,求⊙O的半径.16. 计算:﹣ ﹣|4sin30°﹣ |+(﹣ )﹣117. 解方程:1+18. 如图,已知矩形 中,连接 请利用尺规作图法在对角线 上求作一点 使得 .(保留作图痕迹不写作法)
(1)、求证:DB平分∠ADC;(2)、若EB=10,CD=9,tan∠ABE= ,求⊙O的半径.16. 计算:﹣ ﹣|4sin30°﹣ |+(﹣ )﹣117. 解方程:1+18. 如图,已知矩形 中,连接 请利用尺规作图法在对角线 上求作一点 使得 .(保留作图痕迹不写作法) 19. 如图,已知△ABC是等边三角形,点D在AC边上一点,连接BD,以BD为边在AB的左侧作等边△DEB,连接AE,求证:AB平分∠EAC.
19. 如图,已知△ABC是等边三角形,点D在AC边上一点,连接BD,以BD为边在AB的左侧作等边△DEB,连接AE,求证:AB平分∠EAC. 20. 某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查了部分学生的数学成绩,并将抽样的数据进行了如下整理.(1)、填空 , , 数学成绩的中位数所在的等级.(2)、如果该校有1200名学生参加了本次模拟测,估计 等级的人数;(3)、已知抽样调查学生的数学成绩平均分为102分,求A级学生的数学成绩的平均分数.
20. 某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查了部分学生的数学成绩,并将抽样的数据进行了如下整理.(1)、填空 , , 数学成绩的中位数所在的等级.(2)、如果该校有1200名学生参加了本次模拟测,估计 等级的人数;(3)、已知抽样调查学生的数学成绩平均分为102分,求A级学生的数学成绩的平均分数.①如下分数段整理样本
等级等级
分数段
各组总分
人数
4
843
574
171
2
②根据上表绘制扇形统计图
 21. 如图,小华和同伴在春游期间,发现在某地小山坡的点E处有一棵盛开的桃花的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即DE的长度,小华站在点B的位置,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小华的身高为1.8米,请你利用以上的数据求出DE的长度.(结果保留根号)
21. 如图,小华和同伴在春游期间,发现在某地小山坡的点E处有一棵盛开的桃花的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即DE的长度,小华站在点B的位置,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小华的身高为1.8米,请你利用以上的数据求出DE的长度.(结果保留根号) 22. 小丽和哥哥小明分别从家和图书馆同时出发,沿同一条路相向而行,小丽开始跑步,遇到哥哥后改为步行,到达图书馆恰好用35分钟,小明匀速骑自行车直接回家,骑行10分钟后遇到了妹妺,再继续骑行5分钟,到家两人距离家的路程y(m)与各自离开出发的时间x(min)之间的函数图象如图所示:
22. 小丽和哥哥小明分别从家和图书馆同时出发,沿同一条路相向而行,小丽开始跑步,遇到哥哥后改为步行,到达图书馆恰好用35分钟,小明匀速骑自行车直接回家,骑行10分钟后遇到了妹妺,再继续骑行5分钟,到家两人距离家的路程y(m)与各自离开出发的时间x(min)之间的函数图象如图所示: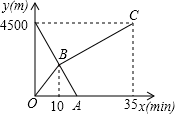 (1)、求两人相遇时小明离家的距离;(2)、求小丽离距离图书馆500m时所用的时间.23. 某超市在春节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣和优惠,在每个转盘中指针指向每个区域的可能性均相同,若指针指向分界线,则重新转动转盘,区域对应的优惠方式如下,A1 , A2 , A3区域分别对应9折8折和7折优惠,B1 , B2 , B3 , B4区域对应不优惠?本次活动共有两种方式.
(1)、求两人相遇时小明离家的距离;(2)、求小丽离距离图书馆500m时所用的时间.23. 某超市在春节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣和优惠,在每个转盘中指针指向每个区域的可能性均相同,若指针指向分界线,则重新转动转盘,区域对应的优惠方式如下,A1 , A2 , A3区域分别对应9折8折和7折优惠,B1 , B2 , B3 , B4区域对应不优惠?本次活动共有两种方式.方式一:转动转盘甲,指针指向折扣区域时,所购物品享受对应的折扣优惠,指针指向其他区域无优惠;
方式二:同时转动转盘甲和转盘乙,若两个转盘的指针均指向折扣区域时,所购物品享受折上折的优惠,其他情况无优惠.
 (1)、若顾客选择方式一,则享受优惠的概率为;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能顾客享受折上折优惠的概率.24. 已知抛物线, 与 轴交于 两点,与 轴交于点 ,且抛物线 的对称轴为直线 .(1)、抛物线的表达式;(2)、若抛物线 与抛物线 关于直线 对称,抛物线 与 轴交于点 两点(点 在点 左侧),要使 ,求所有满足条件的抛物线 的表达式.25. 问题提出
(1)、若顾客选择方式一,则享受优惠的概率为;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能顾客享受折上折优惠的概率.24. 已知抛物线, 与 轴交于 两点,与 轴交于点 ,且抛物线 的对称轴为直线 .(1)、抛物线的表达式;(2)、若抛物线 与抛物线 关于直线 对称,抛物线 与 轴交于点 两点(点 在点 左侧),要使 ,求所有满足条件的抛物线 的表达式.25. 问题提出 (1)、如图1,在△ABC中,∠A=75°,∠C=60°,AC=6 ,求△ABC的外接圆半径R的值;
(1)、如图1,在△ABC中,∠A=75°,∠C=60°,AC=6 ,求△ABC的外接圆半径R的值;问题探究
(2)、如图2,在△ABC中,∠BAC=60°,∠C=45°,AC=8 ,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;问题解决
(3)、如图3,在四边形ABCD中,∠BAD=90°,∠BCD=30°,AB=AD,BC+CD=12 ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.