宁夏中卫市中宁县2020年数学中考一模试卷
试卷更新日期:2020-06-09 类型:中考模拟
一、选择题
-
1. 截止2020年4月24日,世界各国感染新冠状肺炎病毒患者累计确诊达到274万人,将数据274万用科学记数表示为( )
A、 2.74×102 B、2.74×105 C、2.74×106 D、2.74×1072. 下列各式中正确的是( )A、 B、 C、 =±2 D、3. 如图是由3个大小相同的小正方体组成的几何体,它的左视图是( ) A、
A、 B、
B、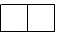 C、
C、 D、
D、 4. 已知 ,则a+b等于( )A、2 B、 C、3 D、15. 为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
4. 已知 ,则a+b等于( )A、2 B、 C、3 D、15. 为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )捐款数额
10
20
30
50
100
人数
2
4
5
3
1
A、众数是100 B、中位数是30 C、极差是20 D、平均数是306. “绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )A、 B、 C、 D、7. 如图,两条直线l1∥l2 , Rt△ACB中,∠C=90°,AC=BC,顶点A,B分别在l1和l2上,∠1=20°,则∠2的度数是( )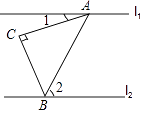 A、45° B、55° C、65° D、75°8. 均匀地向一个容器注水,最后将容器注满 在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是
A、45° B、55° C、65° D、75°8. 均匀地向一个容器注水,最后将容器注满 在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是 A、
A、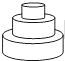 B、
B、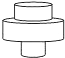 C、
C、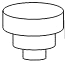 D、
D、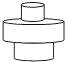
二、填空题
-
9. 分解因式:x3-x= .10. 计算:( )﹣2+| ﹣2|=.11. 七年级某班有50名同学,其中男生28名,女生22名,从中随机选出一名学生做明天的英语值日报告,选中女生的概率是.12. 某品牌的衬衣每件进价是80元,售价为120元,“五•一”期间搞活动打9折,则销售1件衬衣的利润是元13. 若线段CD是由线段AB平移得到的,点A(﹣2,3)的对应点为C(3,6),则点B(﹣5,﹣2)的对应点D的坐标是14. 关于x的一元二次方程(k+1)x2﹣2x+1=0有两个实数根,则k的取值范围是15. 如图,已知反比例函数y=
 (k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B,若△AOB的面积为1,则k=.
(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B,若△AOB的面积为1,则k=. 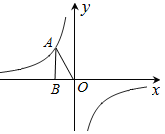 16. 如图,正六边形ABCDEF内接于⊙O , AB=2,则图中阴影部分的面积为
16. 如图,正六边形ABCDEF内接于⊙O , AB=2,则图中阴影部分的面积为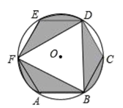
三、解答题
-
17. 先化简,再求值: ,其中18. 解一元一次不等式组:19. 在如图所示的平面直角坐标系中,已知点A(﹣3,﹣3),B(﹣1,﹣3),C(﹣1,﹣1).

①画出△ABC,并画出△ABC关于x轴对称的△A1B1C1
②以O为位似中心,在第一象限内把△ABC扩大到原来的两倍,得到△A2B2C2.
20. 为了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等5项体育活动的喜欢程度,某校随机抽查部分学生,对他们最喜欢的体育项目(每人只选一项)进行了问卷调查,并将统计数据绘制成如下两幅不完整的统计图:请解答下列问题:
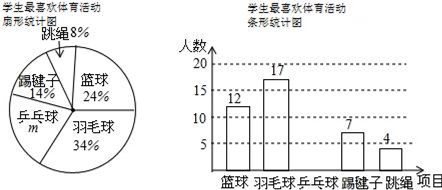 (1)、m=%,这次共抽取了名学生进行调查;请补全条形统计图;(2)、若全校有800名学生,则该校约有多少名学生喜爱打篮球?(3)、学校准备从喜欢跳绳活动的4人(二男二女)中随机选取2人进行体能测试,求抽到一男一女学生的概率是多少?21. 如图,在四边形ABCD中,AD∥BC , BA=BC , BD平分∠ABC .
(1)、m=%,这次共抽取了名学生进行调查;请补全条形统计图;(2)、若全校有800名学生,则该校约有多少名学生喜爱打篮球?(3)、学校准备从喜欢跳绳活动的4人(二男二女)中随机选取2人进行体能测试,求抽到一男一女学生的概率是多少?21. 如图,在四边形ABCD中,AD∥BC , BA=BC , BD平分∠ABC . (1)、求证:四边形ABCD是菱形;(2)、过点D作DE⊥BD , 交BC的延长线于点E , 若BC=5,BD=8,求四边形ABED的周长.22. 为“创建文明城市,构建和谐社会”,更好的提高垃圾分类意识,某小区决定安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和4个垃圾箱共需580元,购买5个温馨提示牌和2个垃圾箱共需500元.(1)、购买1个温馨提示牌和1个垃圾箱各需多少元?(2)、如果需要购买温馨提示牌和垃圾箱共100个,费用不超过8000元,问:最多购买垃圾箱多少个?23. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)、求证:四边形ABCD是菱形;(2)、过点D作DE⊥BD , 交BC的延长线于点E , 若BC=5,BD=8,求四边形ABED的周长.22. 为“创建文明城市,构建和谐社会”,更好的提高垃圾分类意识,某小区决定安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和4个垃圾箱共需580元,购买5个温馨提示牌和2个垃圾箱共需500元.(1)、购买1个温馨提示牌和1个垃圾箱各需多少元?(2)、如果需要购买温馨提示牌和垃圾箱共100个,费用不超过8000元,问:最多购买垃圾箱多少个?23. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.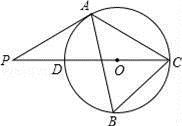 (1)、求证:PA是⊙O的切线;(2)、若PD=1,求⊙O的直径.24. 随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫站的距离为 (单位:km),乘坐地铁的时间 (单位:min)是关于 的一次函数,其关系如下表:
(1)、求证:PA是⊙O的切线;(2)、若PD=1,求⊙O的直径.24. 随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫站的距离为 (单位:km),乘坐地铁的时间 (单位:min)是关于 的一次函数,其关系如下表:地铁站
A
B
C
D
E
x/km
7
9
11
12
13
y1/min
16
20
24
26
28
(1)、求 关于 的函数解析式;(2)、李华骑单车的时间 (单位:min)也受 的影响,其关系可以用 = 2-11 +78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最短时间.25. 如图,二次函数 的图象与 轴交于A,B两点,与y轴交于点C,且关于直线 对称,点A的坐标为(-1,0). (1)、求二次函数的表达式;(2)、连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度.26. 如图在△ABC中,∠C=90°,AC=3cm,BC=4cm,点P是边BC上由B向C运动(不与点B、C重合)的一动点,P点的速度是1cm/s,设点P的运动时间为t,过P点作AC的平行线交AB与点N,连接AP,
(1)、求二次函数的表达式;(2)、连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度.26. 如图在△ABC中,∠C=90°,AC=3cm,BC=4cm,点P是边BC上由B向C运动(不与点B、C重合)的一动点,P点的速度是1cm/s,设点P的运动时间为t,过P点作AC的平行线交AB与点N,连接AP,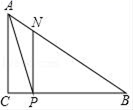 (1)、请用含有t的代数式表示线段AN和线段PN的长,(2)、当t为何值时,△APN的面积等于△ACP面积的三分之一?(3)、在点P的运动过程中,是否存在某一时刻的t的值,使得△APN的面积有最大值,若存在请求出t的值并计算最大面积;若不存在,请说明理由.
(1)、请用含有t的代数式表示线段AN和线段PN的长,(2)、当t为何值时,△APN的面积等于△ACP面积的三分之一?(3)、在点P的运动过程中,是否存在某一时刻的t的值,使得△APN的面积有最大值,若存在请求出t的值并计算最大面积;若不存在,请说明理由.