辽宁省沈阳市皇姑区2020年数学中考一模试卷

试卷更新日期：2020-06-09 类型：中考模拟

进入出卷网下载

一、选择题

1. 在-4、 $- \sqrt{2}$ 、0、4这四个数中，最小的数是（）．

A、4 B、0 C、 $- \sqrt{2}$ D、-4

查看试题解析
2. 天津到上海的铁路里程约1326000米，用科学记数法表示1326000的结果是（）

A、0.1326×10⁷ B、1.326×10⁶ C、13.26×10⁵ D、1.326×10⁷

查看试题解析
3. 如图是由5个小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上的小立方块的个数，则这个几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式中正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $\sqrt[3]{4} = 2$ D、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$

查看试题解析
5. 已知a^m=3，aⁿ=4，则a^m+n的值为（　　）

A、7 B、12 C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析

6. 为了解学生课外阅读时间情况，随机收集了30名学生一天课外阅读时间，整理如下表：

阅读时间/小时	0.5及以下	0.7	0.9	1.1	1.3	1.5及以上
人数	2	9	6	5	4	4

则本次调查中阅读时间的中位数和众数分别是（）

A、0.7和0.7 B、0.9和0.7 C、1和0.7 D、0.9和1.1

查看试题解析

7. 如图，四边形ABCD内接于⊙O，AB是直径，BC∥OD，若∠C＝130°，则∠B的度数为（）

A、50° B、60° C、70° D、80°

查看试题解析
8. 如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法中正确的个数是（）
①AD是∠BAC的平分线；②∠ADC=60°；③点D在AB的垂直平分线上.

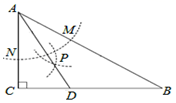A、3 B、2 C、1 D、0

查看试题解析
9. 如图，一艘轮船从位于灯塔C的北偏东方向，距离灯塔60海里的小岛A出发，沿正南方向航行一段时间后，到达位于灯塔C的南偏东方向上的B处，这时轮船B与小岛A的距离是（）

A、 $30 \sqrt{3}$ 海里 B、 $(30 + 30 \sqrt{3})$ 海里 C、120海里 D、60海里

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，以下列结论正确的是（）
① $a b c > 0$ ；② $3 a > 2 b$ ；③ $4 a - 2 b + c < 0$ ；④ $m (a m + b) \leq a - b$ (m为任意实数).

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 因式分解： $9 a b c - 3 a c^{2}$ =.

查看试题解析
12. 计算： $x^{3} \div x =$ .

查看试题解析
13. 如图，下列推理及所证明的理由都正确的是（）

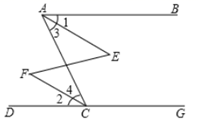A、若 $A B / / D G$ ，则 $∠ B A C = ∠ D C A$ ，理由是内错角相等，两直线平行 B、若 $A B / / D G$ ，则 $∠ 3 = ∠ 4$ ，理由是两直线平行，内错角相等 C、若 $A E / / C F$ ，则 $∠ E = ∠ F$ ，理由是内错角相等，两直线平行 D、若 $A E / / C F$ ，则 $∠ 3 = ∠ 4$ ，理由是两直线平行，内错角相等

查看试题解析
14. 如图，直角△ABC中，∠C=90°，AC=5，BC=12则内部五个小直角三角形的周长的和为.

查看试题解析
15. 如图，已知菱形ABCD的顶点A( $- \sqrt{3}$ ，0)，∠DAB=60°，若动点P从点A出发，沿A→B→C→D→A→B→…的路径，在菱形的边上以每秒0.5个单位长度的速度移动，则第2020秒时，点P的坐标为.

查看试题解析
16. 如图，在△ABC中，∠A＝45°，∠B＝60°，AB＝4，P是BC边上的动点（不与B，C重合），点P关于直线AB，AC的对称点分别为M，N，则线段MN长的取值范围是.

查看试题解析

三、解答题

17. 计算： $6 \sin 45^{°} + | 2 \sqrt{2} - 7 | - {(\frac{1}{2})}^{- 3} + {(2020 - \sqrt{2020})}^{0}$

查看试题解析
18. 一个不透明的口袋中装有4个分别标有数1，2，3，4的小球，它们的形状、大小完全相同，小红先从口袋里随机摸出一个小球记下数为x，小颖在剩下的3个球中随机摸出一个小球记下数为y，这样确定了点P(x，y)，请用“列表法”或“树状图法”求点P(x，y)在函数y=-x+5图象上的概率.

查看试题解析
19. 如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AF=CE，DF=BE，且DF∥BE，过点C作CG⊥AB交AB延长线与点G.

(1)、求证：四边形ABCD是平行四边形；

(2)、若tan∠CAB= $\frac{2}{5}$ ，∠CBG=45°，BC= $4 \sqrt{2}$ ，则ABCD的面积是.

查看试题解析
20. 某商店在开业前，所进三种货物：上衣、裤子和鞋子的数量共480份，这三种货物进货的数量比例如图（1）所示.商店安排6人只销售上衣，4人只销售裤子，2人只销售鞋子，用了5天的时间销售货物的情况如图（2）及表格所示.

货物

上衣(件)

裤子(条)

鞋子(双)

5天的销售总额

150

a

30

(1)、求所进三种货物中上衣有多少件？

(2)、直接在图中把图（2）补充完整；

(3)、表格中的a=(直接填空)；

(4)、若销售人员不变，并以同样的销售速度销售，则上衣、裤子和鞋子中最先销售完的货物为 (直接填空).

查看试题解析
21. 如图，如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，交AC于点E，交AB于点F.

(1)、求证：BC是⊙O的切线；

(2)、若BD= $2 \sqrt{3}$ ，BF=2，求阴影部分的面积 (直接填空).

查看试题解析
22. 如图，在平面直角坐标系中，直线y=x+4与y轴交于点A，与x轴交于点B，直线y=kx+b经过点A，且交x轴与点C(3，0).

(1)、求直线AC的函数表达式；

(2)、动点P在线段CB上由C向B匀速运动，到达点B后停止运动，运动速度为3个单位长度，过点P作PE⊥x轴，交直线AC于点E，过点E作直线GE∥x轴交y轴于点F，交直线AB于点G，设点P的运动时间为t(t＞0)秒.
①直接写出线段PE的长度(用含t的代数式表示)；

②当EG=1时，请直接写出t的值.

查看试题解析
23. 在Rt△ABC中，∠B=90°，BC=4，AB=8，点D是边AC的中点，动点P在边AB上(点P不与点A重合)，连接PD、PC，将△PDC沿直线PD翻折，点C落在点E处得△PDE.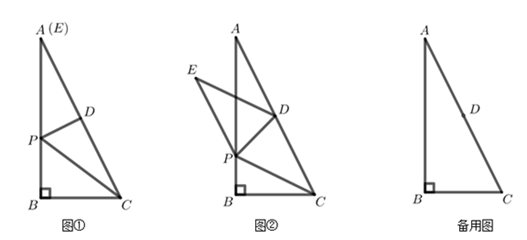

(1)、如图①，若点E恰好与点A重合，求线段AP的长；

(2)、如图②，若ED交AB于点F，四边形CDEP为菱形，求证：△PFE≌△AFD；

(3)、连接AE，设△PDE与△ABC重叠部分的面积为S₁ ， △PAC的面积为S₂ ，若S₁= $\frac{1}{4}$ S₂时，请直接写出tan∠AED的值.

查看试题解析
24. 如图，在平面直角坐标系中，直线 $y = - \frac{5 \sqrt{3}}{11} x + 5 \sqrt{3}$ 与x轴交于点B，与y轴交于点C，抛物线 $y = - \frac{\sqrt{3}}{11} x^{2} + b x + c$ 经过点B和点C，且与x轴交于另一点A，连接AC，点D在BC上方的抛物线上，设点D的横坐标为m，过点D作DH⊥BC于点H.

(1)、求抛物线的函数表达式；

(2)、线段DH的长为 (用含m的代数式表示)；

(3)、点M为线段AC上一点，连接OM绕点O顺时针旋转60°得线段ON，连接CN，当CN= $\sqrt{21}$ ，m=6时，请直接写出此时线段DM的长.

查看试题解析

货物	上衣(件)	裤子(条)	鞋子(双)
5天的销售总额	150	a	30