辽宁省沈阳市2020年数学中考二模试卷

试卷更新日期：2020-06-09 类型：中考模拟

进入出卷网下载

一、选择题

1. 在实数3.14，﹣π， $\frac{1}{3}$ ，﹣ $\sqrt{5}$ 中，倒数最小的数是（）

A、 $- \sqrt{5}$ B、 $\frac{1}{3}$ C、﹣π D、3.14

查看试题解析
2. 据报道，2020年某市户籍人口中，60岁以上的老人有1230000人，预计未来五年该市人口“老龄化”还将提速．将1230000用科学记数法表示为（）

A、12.3×10⁵ B、1.23×10⁵ C、0.12×10⁶ D、1.23×10⁶

查看试题解析
3. 如图所示的是由完全相同的小正方体组成的立体图形，它的左视图为（）

A、 B、 C、 D、

查看试题解析
4. 若 $a^{2} = 4$ ， $b^{2} = 9$ ，且 $a b < 0$ ，则a-b的值为（）

A、 $\pm 5$ B、 $- 2$ C、5 D、 $- 5$

查看试题解析
5. 如图，∠BCD＝95°，AB∥DE，则∠α与∠β满足（）

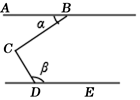A、∠α+∠β＝95° B、∠β﹣∠α＝95° C、∠α+∠β＝85° D、∠β﹣∠α＝85°

查看试题解析
6. 下列事件中，属于必然事件的是（）

A、三角形的外心到三边的距离相等 B、某射击运动员射击一次，命中靶心 C、任意画一个三角形，其内角和是 180° D、抛一枚硬币，落地后正面朝上

查看试题解析
7. 已知多边形的每个内角都是108°，则这个多边形是（）

A、五边形 B、七边形 C、九边形 D、不能确定

查看试题解析
8. 将函数y=﹣3x的图象沿y轴向上平移2个单位长度后，所得图象对应的函数关系式为（）

A、 $y = - 3 x + 2$ B、 $y = - 3 x - 2$ C、 $y = - 3 (x + 2)$ D、 $y = - 3 (x - 2)$

查看试题解析
9. 已知抛物线y=ax²+bx+c的图象如图所示，则关于x的方程ax²+bx+c=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、有两个同号的实数根 D、没有实数根

查看试题解析
10. 如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，其中∠ABC=∠AED=90°，CD与BE、AE分别交于点P、M.对于下列结论：①△CAM∽△DEM；②CD=2BE；③MP•MD=MA•ME；④2CB²=CP•CM.其中正确的是（）

A、①② B、①②③ C、①②③④ D、①③④

查看试题解析

二、填空题

11. 在九年级体育考试中，某校某班参加仰卧起坐测试的8名女生成绩如下（单位：次/分）：44，45，42，48，46，43，47，45，则这组数据的众数为．

查看试题解析
12. 如图，一根直立于水平地面的木杆AB在灯光下形成影子AC（AC＞AB），当木杆绕点A按逆时针方向旋转，直至到达地面时，影子的长度发生变化.已知AE＝5m，在旋转过程中，影长的最大值为5m，最小值3m，且影长最大时，木杆与光线垂直，则路灯EF的高度为 m.

查看试题解析
13. 不等式组 ${\begin{array}{l} 2 - x ⩾ 0 \\ 2 x > x - 1 \end{array}$ 的最小整数解是.

查看试题解析
14. 如图，已知直线y＝﹣x+2分别与x轴，y轴交于A，B两点，与双曲线y＝ $\frac{k}{x}$ 交于E，F两点，若AB＝2EF，则k的值是.

查看试题解析
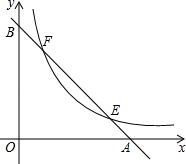15. 如图，A、B、C是小正方形的顶点，且每个小正方形的边长为1，则tan∠BAC的值为.

查看试题解析
16. 如图，平行四边形ABCD中，AB＝3，BC＝2，∠DAB＝60°，E在AB上，且AE＝ $\frac{1}{2}$ EB，F是BC的中点，过D分别作DP⊥AF于P，DQ⊥CE于Q，则DP：DQ的值为.

查看试题解析

三、解答题

17. 先化简，再求值：（2﹣ $\frac{x - 1}{x + 1}$ ）÷ $\frac{x^{2} + 6 x + 9}{x^{2} - 1}$ ，其中x＝ $\sqrt{2}$ ﹣3.

查看试题解析
18. 如图，在矩形ABCD中，E是边AD上一点（不与点A重合），连结BE，PQ垂直平分BE，分别交AD、BE、BC于点P、O、Q，连结BP、EQ.求证：四边形BPEQ是菱形.

查看试题解析
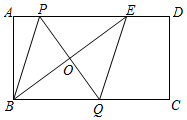19. 在甲口袋中有三个球分别标有数码1，-2，3；在乙口袋中也有三个球分别标有数码4，-5，6；已知口袋均不透明，六个球除标码不同外其他均相同，小明从甲口袋中任取一个球，并记下数码，小林从乙口袋中任取一个球，并记下数码.

(1)、用树状图或列表法表示所有可能的结果；

(2)、求所抽取的两个球数码的乘积为负数的概率.

查看试题解析
20. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利，初二数学小组在校内对“你最认可的四大新生事物”进行了调查，随机调查了 $m$ 人（每名学生必选一种且只能从这四种中选择一种）并将调查结果绘制成如下不完整的统计图．

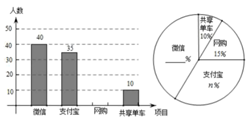(1)、根据图中信息求出 $m$ = ， $n$ =；

(2)、请你帮助他们将这两个统计图补全；

(3)、根据抽样调查的结果，请估算全校2000名学生种，大约有多少人最认可“微信”这一新生事物？

查看试题解析
21. 某网店准备经销一款儿童玩具，每个进价为35元，经市场预测，包邮单价定为50元时，每周可售出200个，包邮单价每增加1元销售将减少10个，已知每成交一个，店主要承付5元的快递费用，设该店主包邮单价定为x(元)(x＞50)，每周获得的利润为y(元).

(1)、求该店主包邮单价定为53元时每周获得的利润；

(2)、求y与x之间的函数关系式；

(3)、该店主包邮单价定为多少元时，每周获得的利润最大？最大值是多少？

查看试题解析
22. 如图，以AB为直径的⊙O交△ABC的边AC于D、BC于E，过D作⊙O的切线交BC于F，交BA延长线于G，且DF⊥BC.

(1)、求证：BA＝BC；

(2)、若AG＝2，cosB＝ $\frac{3}{5}$ ，求DE的长.

查看试题解析
23. 如图①，已知直线y＝﹣2x+4与x轴、y轴分别交于点A、C ，以OA、OC为边在第一象限内作长方形OABC ．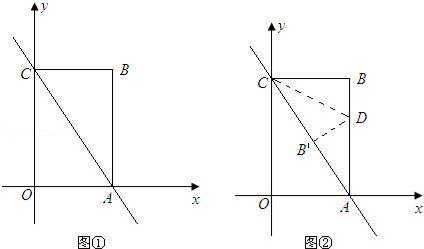

(1)、求点A、C的坐标；

(2)、将△ABC对折，使得点A的与点C重合，折痕交AB于点D ，求直线CD的解析式（图②）；

(3)、在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析
24. 如图1，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点.

(1)、观察猜想：
图1中，线段PM与PN的数量关系是，位置关系是；

(2)、探究证明：
把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；

(3)、拓展延伸：
把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值.

查看试题解析
25. 若二次函数 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴分别交于点 $A (3 ， 0)$ 、 $B (0 ， - 2)$ ，且过点 $C (2 ， - 2)$ .

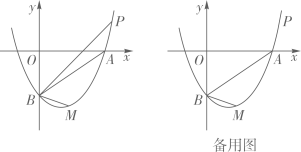(1)、求二次函数表达式；

(2)、若点 $P$ 为抛物线上第一象限内的点，且 $S_{Δ P A B} = 4$ ，求点 $P$ 的坐标；

(3)、在抛物线上（ $A B$ 下方）是否存在点 $M$ ，使 $∠ A B O = ∠ A B M$ ？若存在，求出点 $M$ 到 $y$ 轴的距离；若不存在，请说明理由.

查看试题解析