辽宁省葫芦岛市连山区2020年数学中考三模试卷
试卷更新日期:2020-06-09 类型:中考模拟
一、选择题
-
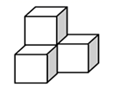
1. 下列各数中最小的数是( )A、 B、 C、 D、2. 下计算正确的是( ).A、 B、 C、 D、3. 下列几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 有五张完全相同的卡片,正面分别画有平行四边形、等边三角形、正五边形、矩形、圆,将它们打乱顺序后背面向上,从中随机选取一张卡片,正面图形既是中心对称图形又是轴对称图形的概率为( )A、 B、 C、 D、5. 如图,多边形ABCDEFG中, ,则 的值为( )
4. 有五张完全相同的卡片,正面分别画有平行四边形、等边三角形、正五边形、矩形、圆,将它们打乱顺序后背面向上,从中随机选取一张卡片,正面图形既是中心对称图形又是轴对称图形的概率为( )A、 B、 C、 D、5. 如图,多边形ABCDEFG中, ,则 的值为( )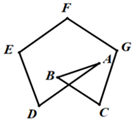 A、 B、 C、 D、6. 如图, 内接于 是 的切线, , . ,则 长为( )
A、 B、 C、 D、6. 如图, 内接于 是 的切线, , . ,则 长为( )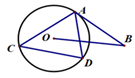 A、 B、 C、 D、7. 关于 的一元二次方程 有实数根,则实数 的取值范围是( )A、 B、 C、 且 D、8. 今年 月,某种口罩单价,上涨 元,同样花费 元买这种口罩,涨价前可以比涨价后多买 个,设涨价后每个口罩 元,可列出的正确的方程是( ).A、 B、 C、 D、9. 如图所示为反比例函数 的部分图象,点 , ,点 为 中点, 交反比例函数的图象于点 , 则 的值为( )
A、 B、 C、 D、7. 关于 的一元二次方程 有实数根,则实数 的取值范围是( )A、 B、 C、 且 D、8. 今年 月,某种口罩单价,上涨 元,同样花费 元买这种口罩,涨价前可以比涨价后多买 个,设涨价后每个口罩 元,可列出的正确的方程是( ).A、 B、 C、 D、9. 如图所示为反比例函数 的部分图象,点 , ,点 为 中点, 交反比例函数的图象于点 , 则 的值为( ) A、 B、 C、 D、10. 如图,四边形 是菱形, ,点 从 点出发,沿 运动,过点 作直线 的垂线,垂足为 ,设点 运动的路程为 , 的面积为 ,则下列图象能正确反映 与 之间的函数关系的是( ).
A、 B、 C、 D、10. 如图,四边形 是菱形, ,点 从 点出发,沿 运动,过点 作直线 的垂线,垂足为 ,设点 运动的路程为 , 的面积为 ,则下列图象能正确反映 与 之间的函数关系的是( ). A、
A、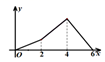 B、
B、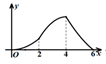 C、
C、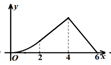 D、
D、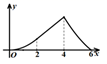
二、填空题
-
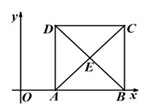
11. 随着人们支付方式的改变,支付宝用户迅猛增加,截至2019年6月,全球支付宝用户超,过 亿.用科学记数法表示数据 亿为12. 将多项式 因式分解为:13. 用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是 .14. 在本学期的五次数学检测中,甲同学的成绩是: ,乙同学的成绩是: ,两名同学成绩比较稳定的是 (填“甲”或“乙”) .15. 如图,在平面直角坐标系中,正方形 的对角线相交于点 ,将正方形 以 为位似中心, 为位似比缩小,点 的对应点 的坐标是
 16. 如图, 为 的 边上的中线,沿 将 折叠,点 的对应点为 ,已知 ,则点 与点 之间的距离是
16. 如图, 为 的 边上的中线,沿 将 折叠,点 的对应点为 ,已知 ,则点 与点 之间的距离是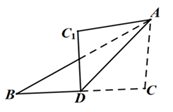 17. 如图, 为等边三角形, 为其内心,射线 交 于点 , 点 为射线 上一动点,将射线 绕点 逆时针旋转 ,与射线 交于点 ,当 时, 的长度为
17. 如图, 为等边三角形, 为其内心,射线 交 于点 , 点 为射线 上一动点,将射线 绕点 逆时针旋转 ,与射线 交于点 ,当 时, 的长度为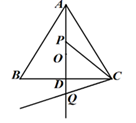 18. 已知关于 的二次函数 的图象开口向下, 与 的部分对应值如下表所示:
18. 已知关于 的二次函数 的图象开口向下, 与 的部分对应值如下表所示:下列判断,① ;② ;③方程 有两个不相等的实数根;
④若 ,则 ,正确的是(填写正确答案的序号) .
三、解答题
-
19. 先化简,再求值: ,其中20. 某中学现有的五个社团: .文学, .辩论, .体育, .奥数, .围棋,为了选出“你最喜爱的社团”,在部分同学中开展了调查( 每名被调查的同学必须且只能选出一个社团),并将调查结果进行了统计,绘制了如下两幅不完整的统计图:
 (1)、求本次被调查的人数;(2)、将上面两幅统计图补充完整;(3)、若该学校大约有学生 人,请你估计喜欢体育社团的人数;(4)、学校为社团安排了 号教室供社团活动使用,文学设社和辩论社使用的教室恰好相邻的概率是多少?21. 元旦联欢会前,班级买了甲、乙、丙三种笔记本作为奖品,共买了 本,花了 元,其中乙种笔记本数量是甲种笔记本数量的 倍,已知甲种笔记本单价为 元,乙种笔记本单价为 元,丙种笔记本单价为 元.(1)、求甲、乙、丙三种笔记本各买了多少本?(2)、若购买奖品的费用又增加了 元,且购买奖品的总数量及购买乙种笔记本数量不变,则最多可以购买甲型笔记本多少本?22. 如图,等腰 中, 是 的角平分线, 交 于点 ,点 为 中点,连接 ,若
(1)、求本次被调查的人数;(2)、将上面两幅统计图补充完整;(3)、若该学校大约有学生 人,请你估计喜欢体育社团的人数;(4)、学校为社团安排了 号教室供社团活动使用,文学设社和辩论社使用的教室恰好相邻的概率是多少?21. 元旦联欢会前,班级买了甲、乙、丙三种笔记本作为奖品,共买了 本,花了 元,其中乙种笔记本数量是甲种笔记本数量的 倍,已知甲种笔记本单价为 元,乙种笔记本单价为 元,丙种笔记本单价为 元.(1)、求甲、乙、丙三种笔记本各买了多少本?(2)、若购买奖品的费用又增加了 元,且购买奖品的总数量及购买乙种笔记本数量不变,则最多可以购买甲型笔记本多少本?22. 如图,等腰 中, 是 的角平分线, 交 于点 ,点 为 中点,连接 ,若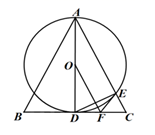 (1)、求证: 是 的切线;(2)、连接 ,若 ,求 的半径.23. 如图,在教室前面墙壁 处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点 时,摄像头俯角约为 ,受安装支架限制,摄像头观测的俯角最大约为 ,已知摄像头安装点高度 约为 米,摄像头与安装的墙壁之间距离忽略不计,
(1)、求证: 是 的切线;(2)、连接 ,若 ,求 的半径.23. 如图,在教室前面墙壁 处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点 时,摄像头俯角约为 ,受安装支架限制,摄像头观测的俯角最大约为 ,已知摄像头安装点高度 约为 米,摄像头与安装的墙壁之间距离忽略不计,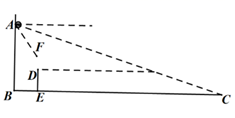 (1)、求教室的长(教室前后墙壁之间的距离 的值);(2)、若第一排桌子前边缘与前面墙壁的距离 为 米, 桌子的高度 为 米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? ( ,精确到 米)24. “武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了 条口罩生产线,每条生产线每天可生产口罩 个.如果每增加一条生产线,每条生产线就会比原来少生产 个口罩.设增加 条生产线后,每条生产线每天可生产口罩 个.(1)、直接写出 与 之间的函数关系式;(2)、若每天共生产口罩 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?(3)、设该厂每天可以生产的口罩 个,请求出 与 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?25. 在 中, ,点 为底边 上一动点,将射线 绕点 逆时针旋转后,与射线 相交于点 ,且(1)、如图①,当点 在底边 上, 时,请直接写出线段 之间的数量关系;
(1)、求教室的长(教室前后墙壁之间的距离 的值);(2)、若第一排桌子前边缘与前面墙壁的距离 为 米, 桌子的高度 为 米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? ( ,精确到 米)24. “武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了 条口罩生产线,每条生产线每天可生产口罩 个.如果每增加一条生产线,每条生产线就会比原来少生产 个口罩.设增加 条生产线后,每条生产线每天可生产口罩 个.(1)、直接写出 与 之间的函数关系式;(2)、若每天共生产口罩 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?(3)、设该厂每天可以生产的口罩 个,请求出 与 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?25. 在 中, ,点 为底边 上一动点,将射线 绕点 逆时针旋转后,与射线 相交于点 ,且(1)、如图①,当点 在底边 上, 时,请直接写出线段 之间的数量关系;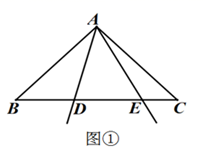 (2)、如图②,当点 在底边 上, ,且 时,求证:
(2)、如图②,当点 在底边 上, ,且 时,求证: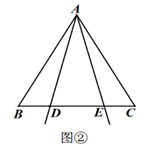 (3)、当 ,且 时,请直接写出 的值.
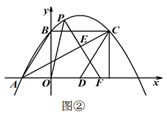
(3)、当 ,且 时,请直接写出 的值.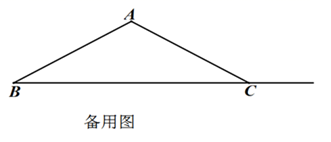 26. 如图①,直线 与 轴、 轴分别交于 两点,将 沿 轴正方向平移后,点 、点 的对应点分别为点 、点 ,且四边形 为菱形,连接 ,抛物线 经过 三点,点 为 上方抛物线上一动点,作 ,垂足为
26. 如图①,直线 与 轴、 轴分别交于 两点,将 沿 轴正方向平移后,点 、点 的对应点分别为点 、点 ,且四边形 为菱形,连接 ,抛物线 经过 三点,点 为 上方抛物线上一动点,作 ,垂足为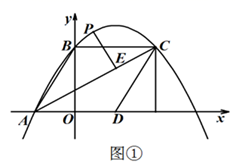 (1)、求此抛物线的函数关系式;(2)、求线段 长度的最大值;(3)、如图②,延长 交 轴于点 ,连接 ,若 为等腰三角形,请直接写出点 的坐标.
(1)、求此抛物线的函数关系式;(2)、求线段 长度的最大值;(3)、如图②,延长 交 轴于点 ,连接 ,若 为等腰三角形,请直接写出点 的坐标.