江苏省宜兴市2020年数学中考一模试卷

试卷更新日期：2020-06-09 类型：中考模拟

进入出卷网下载

一、选择题

1. cos30°=（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
2. 下列式子中，计算正确的是（）

A、m²＋m²=m⁴ B、(m＋2)²=m²＋4 C、(2mn²)³=6m³n⁶ D、5m²n³÷( $\frac{1}{2}$ mn)=10mn²

查看试题解析
3. 下列说法正确的是（）

A、篮球队员在罚球线上投篮一次，则“投中”是随机事件 B、明天的降水概率为 $40 %$ ，则“明天下雨”是确定事件 C、任意抛掷一枚质地均匀的硬币10次，则“有5次正面朝上”是必然事件 D、 $a$ 是实数，则“ $| a | \geq 0$ ”是不可能事件

查看试题解析
4. 一个正多边形的每个外角都等于36°，那么它是（）

A、正六边形 B、正八边形 C、正十边形 D、正十二边形

查看试题解析
5. 若一个三角形的两边长分别为2和6，第三边是方程x²－10x＋21＝0的一根，则这个三角形的周长为（）

A、7 B、3或7 C、15 D、11或15

查看试题解析
6. 在平面直角坐标系中，若点M（m，n）与点Q（－2，3）关于原点对称，则点P（m－n，n）所在象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 圆锥的底面半径为1，母线长为3，则该圆锥侧面积为（）

A、3 B、6π C、3π D、6

查看试题解析
8. 如图，△ABC内接于⊙O，将 $\overset{⌢}{B C}$ 沿BC翻折， $\overset{⌢}{B C}$ 交AC于点D，连接BD，若∠BAC＝66°，则∠ABD的度数是（）

A、66 B、44 C、46 D、48

查看试题解析
9. 如图，在△ABC中，E，G分别是AB，AC上的点，∠AEG=∠C，∠BAC的平分线AD交EG于点F，若 $\frac{A F}{D F} = \frac{3}{2}$ ，则（）

A、 $\frac{A E}{B E} = \frac{3}{5}$ B、 $\frac{E F}{F G} = \frac{2}{3}$ C、 $\frac{E F}{C D} = \frac{3}{5}$ D、 $\frac{E G}{B C} = \frac{2}{3}$

查看试题解析
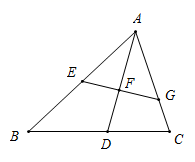10. 如图，已知矩形ABCD的四个顶点都在双曲线y＝ $\frac{k}{x}$ （k＞0）上，BC＝2AB，且矩形ABCD的面积是32，则k的值是（）

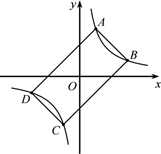A、6 B、8 C、10 D、12

查看试题解析

二、填空题

11. 分解因式： $m^{3} - 4m =$ ．

查看试题解析
12. 函数y= $\sqrt{x - 2}$ 中，自变量x的取值范围是；实数2﹣ $\sqrt{3}$ 的倒数是．

查看试题解析
13. 举世瞩目的港珠澳大桥工程总投资约726亿元，请将数据726亿元用科学记数法表示为元.

查看试题解析
14. 方程组 ${\begin{array}{l} 3 x + 2 y = 8 \\ 2 x - y = 3 \end{array}$ 的解是.

查看试题解析
15. 已知二次函数 $y = a x^{2} - 2 x + 1$ 的图象与x轴只有一个公共点，则a的值是.

查看试题解析
16. 已知平面直角坐标系xOy中，O(0，0)，A(－6，8)，B(m， $- \frac{4}{3}$ m－4)，则平行四边形OABD的面积是.

查看试题解析
17. 如图，正方形ABCD的边长为4，E为AB的中点，将△ADE沿直线DE折叠后，点A落在点F处，DF交对角线AC于G，则FG的长是.

查看试题解析
18. 如图，已知⊙O的半径是2，点A，B在⊙O上，且∠AOB＝90°，动点C在⊙O上运动（不与A，B重合），点D为线段BC的中点，连接AD，则线段AD的长度最大值是.

查看试题解析

三、解答题

19.

(1)、计算： ${(π - 2020)}^{0} + 4 \sin 45 ° - \sqrt{18}$ ；

(2)、化简： $1 - \frac{x^{2} - 2 x}{x^{2} - 1} \div \frac{x - 2}{x - 1}$ .

查看试题解析
20.

(1)、解不等式组： ${\begin{array}{l} 2 x + 1 > x - 1 \\ x - 1 \leq \frac{1}{3} (2 x - 1) \end{array}$ ；

(2)、解方程： $\frac{2 x}{x - 1} - \frac{1}{x} = 2$ .

查看试题解析
21. 已知：如图，点E，D，B，F在同一条直线上，AD∥CB，∠BAD＝∠BCD，DE＝BF.

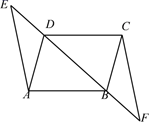
求证：

(1)、AD＝BC；

(2)、AE∥CF

查看试题解析
22. 中考体育测试前，某区教育局为了了解选报引体向上的初三男生的成绩情况，随机抽取了本区部分选报引体向上项目的初三男生的成绩，并将测试得到的成绩绘成了下面两幅不完整的统计图：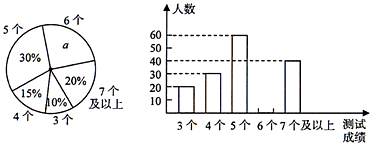

请你根据图中的信息，解答下列问题：

(1)、写出扇形图中 $a =$ ，并补全条形图；

(2)、样本数据的平均数是，众数是，中位数是；

(3)、该区体育中考选报引体向上的男生共有1200人，如果体育中考引体向上达6个以上（含6个）得满分，请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名？

查看试题解析
23. 一个不透明袋子中有 $1$ 个红球， $1$ 个绿球和 $n$ 个白球，这些球除颜色外无其他差别，

(1)、当 $n = 1$ 时，从袋中随机摸出 $1$ 个球，摸到红球和摸到白球的可能性(填“相同”或“不相同”)；

(2)、从袋中随机摸出一个球，记录其颜色，然后放回，大量重复该实验，发现摸到绿球的频率稳定于 $\frac{1}{4}$ ，则 $n$ 的值是；

(3)、在（2）的情况下，如果一次摸出两个球，请用树状图或列表法求摸出的两个球颜色不同的概率.

查看试题解析
24. 如图，AB是⊙O的直径，点C是⊙O上一点，AC平分∠DAB，直线DC与AB的延长线相交于点P，AD与PC延长线垂直，垂足为D，CE平分∠ACB，交⊙O于E.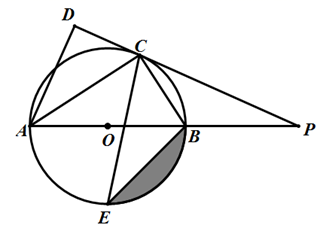

(1)、求证：PC与⊙O相切；

(2)、若AC=6，tan∠BEC= $\frac{2}{3}$ ，求BE的长度以及图中阴影部分面积.

查看试题解析
25. 实行垃圾资源化利用，是社会文明水平的一个重要体现.某环保公司研发的甲、乙两种智能设备可利用最新技术将干垃圾变身为燃料棒.某垃圾处理厂从环保公司购入以上两种智能设备，若干已知购买甲型智能设备花费360万元，购买乙型智能设备花费480万元，购买的两种设备数量相同，且两种智能设备的单价和为140万元.

(1)、求甲乙两种智能设备单价；

(2)、垃圾处理厂利用智能设备生产燃料棒，并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成，其中物资成本占总成本的40%，且生产每吨燃料棒所需人力成本比物资成本的 $\frac{5}{4}$ 倍还多10元，调查发现：若燃料棒售价为每吨200元，平均每天可售出350吨，而当销售价每降低1元，平均每天可多售出5吨，但售价在每吨200元基础上降价幅度不超过7%，
①垃圾处理厂想使这种燃料棒的销售利润平均每天达到36080元，求每吨燃料棒售价应为多少元？

②每吨燃料棒售价应为多少元时，这种燃料棒平均每天的销售利润最大？最大利润是多少？

查看试题解析
26.

(1)、如图1，在⊙O中，AB是直径，弦EF∥AB，在直径AB下方的半圆上有一个定点H（点H不与点A，B重合），请仅用无刻度的直尺画出劣弧 $\overset{⌢}{EF}$ 的中点P，并在直线AB上画出点G，使直线AB平分∠HGP.（保留作图痕迹，不写作法）

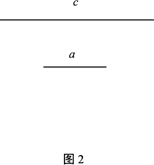(2)、尺规作图：如图2，已知线段a、c，请你用两种不同的方法作Rt△ABC，使其斜边AB=c，一条直角边BC=a.（保留作图痕迹，不写作法）

查看试题解析
27. 在平面直角坐标系中，抛物线 $y = m x^{2} - 4 m x + n$ （m>0）与x轴交于A，B两点，点B在点A的右侧，顶点为C，抛物线与y轴交于点D，直线CA交y轴于E，且 $S_{Δ A B C} ： S_{Δ B C E} = 3 ： 4$ .

(1)、求点A，点B的坐标；

(2)、将△BCO绕点C逆时针旋转一定角度后，点B与点A重合，点O恰好落在y轴上，
①求直线CE的解析式；

②求抛物线的解析式.

查看试题解析
28. 如图1，平面直角坐标系xOy中，A(－4，3)，反比例函数 $y = \frac{k}{x} (k < 0)$ 的图象分别交矩形ABOC的两边AC，BC于E，F（E，F不与A重合），沿着EF将矩形ABOC折叠使A，D重合.

(1)、①如图2，当点D恰好在矩形ABOC的对角线BC上时，求CE的长；
②若折叠后点D落在矩形ABOC内（不包括边界），求线段CE长度的取值范围.

(2)、若折叠后，△ABD是等腰三角形，请直接写出此时点D的坐标.

查看试题解析