江苏省苏州市太仓市2020年数学中考模拟试卷（3月）

试卷更新日期：2020-06-09 类型：中考模拟

进入出卷网下载

一、选择题

1. $\frac{1}{2}$ 的倒数是（）

A、 B、 $- 2$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列运算正确的是（）

A、a²·a³=a⁶ B、(a²)³=a⁶ C、a²+ a³= a⁵ D、a²÷a³=a

查看试题解析
3. 2019年岁末，新冠病毒肆虐中国，极大的危害了人民群众的生命健康，据统计，截至2020年3月28日23时中国累计确诊人数约为83000人，83000用科学记数法可表示为（）

A、 83×10³ B、8.3×10³ C、8.3×10⁴ D、0.83×10⁵

查看试题解析
4. 体育课上五名同学一分钟跳绳个数如下：126，130，132，134，130.则这组数据的众数和中位数是（）

A、130，130 B、130，131 C、134，132 D、131，130

查看试题解析
5. 正比例函数y＝2x的图象向左平移1个单位后所得函数解析式为（）

A、y＝2x+1 B、y＝2x﹣1 C、y＝2x+2 D、y＝2x﹣2

查看试题解析
6. 如图所示，有一个角为30°直角三角板放置在一透明的长直尺上，若∠2＝15°，则∠1度数为（）

A、85° B、75° C、65° D、45°

查看试题解析
7. 下列函数中，函数值y随自变量x增大而减小的是（）

A、y＝2x B、 $y = \frac{1}{2} x + 1$ C、 $y = \frac{2}{x}$ D、y＝﹣x²+2x﹣1（x>1）

查看试题解析
8. 若点Α $(m, n)$ 在一次函数y=3x+b的图象上,且3m-n>2,则b的取值范围为（）

A、b>2 B、b>-2 C、b<2 D、b<-2

查看试题解析
9. 小强从如图所示的二次函数y＝ax²+bx+c的图象中，观察得出了下面五条结论：你认为其中正确结论的个数有（）
（ 1 ）a＜0；（2）b＞0；（3）a﹣b+c＞0；（4）2a+b＜0.

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在梯形ABCD中，AD∥BC，EF是梯形ABCD的中位线，若△BEF的面积为4cm² ，则梯形ABCD的面积为（）

A、8cm² B、12cm² C、16cm² D、20cm²

查看试题解析

二、填空题

11. 当x＝时，分式 $\frac{x^{2} - 4}{x^{2} - 2 x}$ 的值为零.

查看试题解析
12. 分解因式：ax²﹣2ax+a= ．

查看试题解析
13. 已知a，b是一元二次方程x²﹣2x﹣2020＝0的两个根，则a²+2b﹣3的值等于.

查看试题解析
14. 关于x的一元二次方程x²﹣2x+m＝0有两个实数根，则m的取值范围是.

查看试题解析
15. 如图所示，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2，CD平分∠ACB，则 $\frac{S_{△ A C D}}{S_{△ B C D}}$ 值等于.

查看试题解析
16. 如图，已知点A在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上，作 $R t △ A B C$ ，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，若 $△ B C E$ 的面积为6，则k=.

查看试题解析
17. 如图所示，等边△ABC的边长为4，点D是BC边上一动点，且CE＝BD，连接AD，BE，AD与BE相交于点P，连接PC.则线段PC的最小值等于.

查看试题解析

三、解答题

18. 计算：

(1)、 $| - 2 | - {(1 + \sqrt{2})}^{0} + \sqrt{4}$ ；

(2)、 $(a - \frac{1}{a}) \div \frac{a^{2} - 2 a + 1}{a}$ .

查看试题解析
19. 已知|a－1|＋ $\sqrt{b + 2}$ ＝0,求方程 $\frac{a}{x}$ ＋bx＝1的解.

查看试题解析
20. 一家医院某天出生了3个婴儿，假设生男生女的机会相同，那么这3个婴儿中，出现1个男婴、2个女婴的概率是多少？

查看试题解析
21. 如图，已知抛物线y＝x²﹣4与x轴交于点A，B（点A位于点B的左侧），C为顶点，直线y＝x+m经过点A，与y轴交于点D.

(1)、求线段AD的长；

(2)、沿直线AD方向平移该抛物线得到一条新拋物线，设新抛物线的顶点为C'，若点C'在反比例函数 $y = - \frac{3}{x}$ （x＜0）的图象上.求新抛物线对应的函数表达式.

查看试题解析
22.
甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．

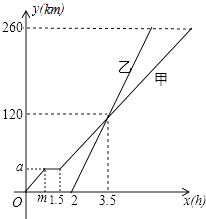(1)、求出图中m，a的值；

(2)、求出甲车行驶路程y（km）与时间x（h）的函数解析式，并写出相应的x的取值范围；

(3)、当乙车行驶多长时间时，两车恰好相距50km．

查看试题解析
23. 如图，在以线段AB为直径的⊙O上取一点，连接AC、BC，将△ABC沿AB翻折后得到△ABD

(1)、试说明点D在⊙O上；

(2)、在线段AD的延长线上取一点E，使AB²=AC·AE，求证：BE为⊙O的切线；

(3)、在（2）的条件下，分别延长线段AE、CB相交于点F，若BC=2，AC=4，求线段EF的长.

查看试题解析
24. 如图，在正方形ABCD中，AB＝10cm，E为对角线BD上一动点，连接AE，CE，过E点作EF⊥AE，交直线BC于点F.E点从B点出发，沿着BD方向以每秒2cm的速度运动，当点E与点D重合时，运动停止.设△BEF的面积为ycm² ， E点的运动时间为x秒.

(1)、求证：CE＝EF；

(2)、求y与x之间关系的函数表达式，并写出自变量x的取值范围；

(3)、求△BEF面积的最大值.

查看试题解析