江苏省昆山九校联考2020年数学中考模拟试卷
试卷更新日期:2020-06-09 类型:中考模拟
一、选择题
-
1. 的绝对值是( )A、 B、 C、 D、2. 港珠澳大桥全长55千米,工程项目总投资额1269亿元,用科学记数法表示1269亿为( )A、 B、 C、 D、3. 长沙某抗战纪念馆馆长联系某中学,选择18名青少年志愿者在同日参与活动,年龄如表所示:这18名志愿者年龄的众数和中位数分别是( )
年龄(单位:岁)
12
13
14
15
人数
3
5
6
4
A、13,14 B、14,14 C、14,13 D、14,154. 如图是由5个相同的小正方体组成的立体图形,它的俯视图是( )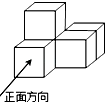 A、
A、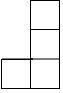 B、
B、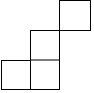 C、
C、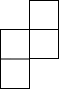 D、
D、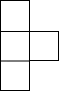 5. 如图,在 中, , , 与 相切于点 , 与 , 分别相交于点E,F,则阴影部分的面积是( )
5. 如图,在 中, , , 与 相切于点 , 与 , 分别相交于点E,F,则阴影部分的面积是( )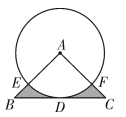 A、 B、 C、 D、6. 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A、 B、 C、 D、6. 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.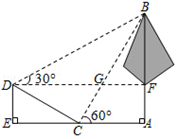 A、10 B、15 C、15 D、15 ﹣57. 已知点M(m,2018),N(n,2018)是二次函数y=ax2+bx+2017图象上的两个不同的点,则当x=m+n时,其函数值y=( )A、2019 B、2018 C、2017 D、20168. 已知t为正整数,关于x的不等式组 的整数解的个数不可能为( )A、16 B、17 C、18 D、199. 如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=4,AF=6,则AC的长为( )
A、10 B、15 C、15 D、15 ﹣57. 已知点M(m,2018),N(n,2018)是二次函数y=ax2+bx+2017图象上的两个不同的点,则当x=m+n时,其函数值y=( )A、2019 B、2018 C、2017 D、20168. 已知t为正整数,关于x的不等式组 的整数解的个数不可能为( )A、16 B、17 C、18 D、199. 如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=4,AF=6,则AC的长为( )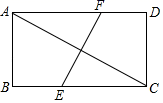 A、4 B、6 C、2 D、10. 已知⊙O的半径为2,A为圆内一定点,AO=1.P为圆上一动点,以AP为边作等腰△APG,AP=PG,∠APG=120°,OG的最大值为( )
A、4 B、6 C、2 D、10. 已知⊙O的半径为2,A为圆内一定点,AO=1.P为圆上一动点,以AP为边作等腰△APG,AP=PG,∠APG=120°,OG的最大值为( ) A、1+ B、1+2 C、2+ D、2 ﹣1
A、1+ B、1+2 C、2+ D、2 ﹣1二、填空题
-
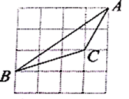
11. 分解因式: .12. 若 有意义,则x的取值范围.13. a是方程x2+x﹣1=0的一个根,则代数式﹣2a2﹣2a+2020的值是14. 如图,在 的正方形方格图形中,小正方形的顶点称为格点, 的顶点都在格点上,则 的余弦值是 .
 15. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为度.
15. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为度.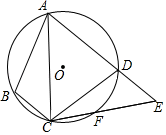 16. 一个圆锥的侧面展开图半径为16cm,圆心角270°的扇形,则这个圆锥的底面半径是cm。17. 如图,在平面直角坐标系中,正方形ABCD的面积为20,顶点A在y轴上,顶点C在x轴上,顶点D在双曲线 的图象上,边CD交y轴于点E,若 ,则k的值为.
16. 一个圆锥的侧面展开图半径为16cm,圆心角270°的扇形,则这个圆锥的底面半径是cm。17. 如图,在平面直角坐标系中,正方形ABCD的面积为20,顶点A在y轴上,顶点C在x轴上,顶点D在双曲线 的图象上,边CD交y轴于点E,若 ,则k的值为.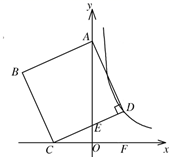 18. 如图,已知在△ABC中,AB=AC=13,BC=10,点M是AC边上任意一点,连接MB,以MB、MC为邻边作平行四边形MCNB,连接MN,则MN的最小值是
18. 如图,已知在△ABC中,AB=AC=13,BC=10,点M是AC边上任意一点,连接MB,以MB、MC为邻边作平行四边形MCNB,连接MN,则MN的最小值是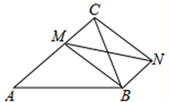
三、解答题
-
19. 计算:(﹣1)2016+2sin60°﹣|﹣ |+π0 .20. 解不等式组,并写出该不等式组的所有整数解.21. 先化简,再求值: ,其中x= .22. 甲、乙两辆货车分别从A、B两城同时沿高速公路向C城运送货物.已知A、C两城相距450千米,B、C两城的路程为440千米,甲车比乙车的速度快10千米/小时,甲车比乙车早半小时到达C城.求两车的速度.23. 为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
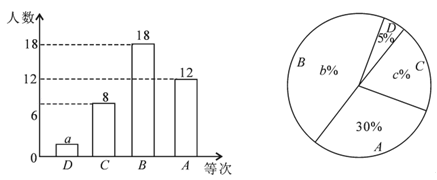 (1)、a= , b= , c=;
(1)、a= , b= , c=;
(2)、扇形统计图中表示C等次的扇形所对的圆心角的度数为度;
(3)、学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.24. 如图,在等腰Rt△ABC中,∠C=90°,AC=4,矩形DEFG的顶点D、G分别在AC、BC上,边EF在AB上. (1)、求证:△AED∽△DCG;(2)、若矩形DEFG的面积为4,求AE的长.25. 如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数 的图像交于A,P两点.
(1)、求证:△AED∽△DCG;(2)、若矩形DEFG的面积为4,求AE的长.25. 如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数 的图像交于A,P两点.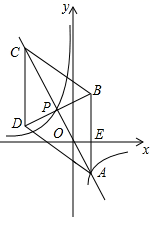 (1)、求m,n的值与点A的坐标(2)、求 的值26. 如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F
(1)、求m,n的值与点A的坐标(2)、求 的值26. 如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F (1)、求证: = ;(2)、若CE=1,EB=3,求⊙O的半径;(3)、若BD=6,AB=10,求D E的长.27. 在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.
(1)、求证: = ;(2)、若CE=1,EB=3,求⊙O的半径;(3)、若BD=6,AB=10,求D E的长.27. 在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.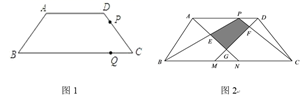 (1)、梯形ABCD的面积等于.(2)、如图1,动点P从D点出发沿DC以DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.当PQ∥AB时,P点离开D点多少时间?(3)、如图2,点K是线段AD上的点,M、N为边BC上的点,BM=CN=5,连接AN、DM,分别交BK、CK于点E、F,记△ ADG和△ BKC重叠部分的面积为S,求S的最大值.28. 如图①,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)经过点D(2,4),与x轴交于A,B两点,与y轴交于点C(0,4),连接AC,CD,BC, 其且AC=5.
(1)、梯形ABCD的面积等于.(2)、如图1,动点P从D点出发沿DC以DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.当PQ∥AB时,P点离开D点多少时间?(3)、如图2,点K是线段AD上的点,M、N为边BC上的点,BM=CN=5,连接AN、DM,分别交BK、CK于点E、F,记△ ADG和△ BKC重叠部分的面积为S,求S的最大值.28. 如图①,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)经过点D(2,4),与x轴交于A,B两点,与y轴交于点C(0,4),连接AC,CD,BC, 其且AC=5.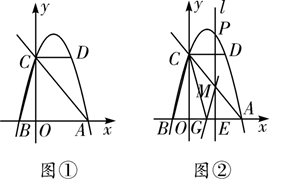 (1)、求抛物线的解析式;(2)、如图②,点P是抛物线上的一个动点,过点P作x轴的垂线l,l分别交x轴于点E,交直线AC于点M.设点P的横坐标为m.当0<m≤2时,过点M作MG∥BC,MG交x轴于点G,连接GC,则m为何值时,△GMC的面积取得最大值,并求出这个最大值;(3)、当-1<m≤2时,是否存在实数m,使得以P,C,M为顶点的三角形和△AEM相似?若存在,求出相应m的值;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图②,点P是抛物线上的一个动点,过点P作x轴的垂线l,l分别交x轴于点E,交直线AC于点M.设点P的横坐标为m.当0<m≤2时,过点M作MG∥BC,MG交x轴于点G,连接GC,则m为何值时,△GMC的面积取得最大值,并求出这个最大值;(3)、当-1<m≤2时,是否存在实数m,使得以P,C,M为顶点的三角形和△AEM相似?若存在,求出相应m的值;若不存在,请说明理由.