江苏省盐城市阜宁县2020年九年级第一次调研数学试卷
试卷更新日期:2020-06-09 类型:中考模拟
一、选择题
-
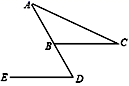
1. 2的相反数是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,点D在△ABC的边AB的延长线上,DE∥BC,若∠A=32°,∠C=26°,则∠D的度数是( )
 A、58° B、59° C、60° D、69°4. 函数 中,自变量x的取值范围是( )A、x≠0 B、x<1 C、x>1 D、x≠15. 若a<b,则下列结论不一定成立的是( )A、a-1<b-1 B、2a<2b C、 D、a2<b26. 如图,已知AB是⊙O的直径,点C,D在⊙O上,弧AC的度数为100°,则∠D的大小为( )
A、58° B、59° C、60° D、69°4. 函数 中,自变量x的取值范围是( )A、x≠0 B、x<1 C、x>1 D、x≠15. 若a<b,则下列结论不一定成立的是( )A、a-1<b-1 B、2a<2b C、 D、a2<b26. 如图,已知AB是⊙O的直径,点C,D在⊙O上,弧AC的度数为100°,则∠D的大小为( ) A、30° B、40° C、50° D、60°7. 如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )。
A、30° B、40° C、50° D、60°7. 如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )。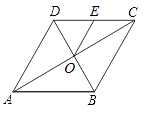 A、 B、2 C、 D、48. 规定用符号 表示实数 的整数部分,例如 ,按此规定, 的值为( )A、6 B、5 C、4 D、3
A、 B、2 C、 D、48. 规定用符号 表示实数 的整数部分,例如 ,按此规定, 的值为( )A、6 B、5 C、4 D、3二、填空题
-
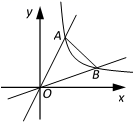
9. 一组数据:2,5,3,1,6,则这组数据的中位数是.10. 约翰斯·霍普金斯大学新冠肺炎疫情统计数据显示,截至北京时间4月13日06时30分,全球新冠肺炎确诊病例超184万例,将1840000用科学记数法表示是.11. 分解因式:2a2-2=.12. 若一个正多边形的内角和是其外角和的3倍,则这个多边形的边数是 .13. 已知圆锥的底面圆半径为3cm,高为4cm,则圆锥的侧面积是cm2.14. 在平面直角坐标系中,将点(1,-2)先向右平移2个单位长度,再向上平移3个单位长度,则所得的点的坐标是.15. 为了改善生态环境,防止水土流失,红旗村计划在荒坡上种树960棵,由于青年志愿者支援,实际每天种树的棵数是原计划的2倍,结果提前4天完成任务,则原计划每天种树的棵数是.16. 如图,在平面直角坐标系中,反比例函数 与正比例函数 的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是.
 17. 计算(-3)2+20200- .18. 解方程: ﹣ =019. 解不等式组并将其解集在数轴上表示: .20. 小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
17. 计算(-3)2+20200- .18. 解方程: ﹣ =019. 解不等式组并将其解集在数轴上表示: .20. 小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:项目
月功能费
基本话费
长途话费
短信费
金额/元
5
▲
▲
25
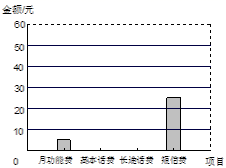
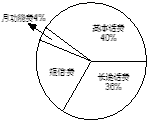 (1)、该月小王手机话费共有多少元?(2)、扇形统计图中,表示短信费的扇形的圆心角为多少度?(3)、请将表格补充完整;(4)、请将条形统计图补充完整.21. 端午节是我国传统佳节.小峰同学带了4个粽子(除粽馅不同外,其它均相同),其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子,准备从中任意拿出两个送给他的好朋友小悦.(1)、用树状图或列表的方法列出小悦拿到两个粽子的所有可能结果;(2)、请你计算小悦拿到的两个粽子都是肉馅的概率.22. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)、该月小王手机话费共有多少元?(2)、扇形统计图中,表示短信费的扇形的圆心角为多少度?(3)、请将表格补充完整;(4)、请将条形统计图补充完整.21. 端午节是我国传统佳节.小峰同学带了4个粽子(除粽馅不同外,其它均相同),其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子,准备从中任意拿出两个送给他的好朋友小悦.(1)、用树状图或列表的方法列出小悦拿到两个粽子的所有可能结果;(2)、请你计算小悦拿到的两个粽子都是肉馅的概率.22. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.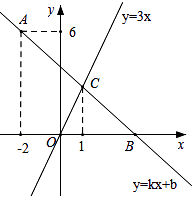 (1)、求k、b的值;(2)、若点D在y轴负半轴上,且满足S△COD= S△BOC , 求点D的坐标.23. 为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据: ≈1.414, ≈1.732)
(1)、求k、b的值;(2)、若点D在y轴负半轴上,且满足S△COD= S△BOC , 求点D的坐标.23. 为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据: ≈1.414, ≈1.732)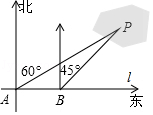 24. 如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
24. 如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.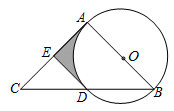 (1)、试判断直线DE与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.25. 某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.(1)、当销售该纪念品每天能获得利润2160元时,每件的销售价应为多少?(2)、当每件的销售价为多少时,销售该纪念品每天获得的利润最大?并求出最大利润.26. 已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD所在的直线对折,使点B落在点B′处,连结AB',BB',延长CD交BB'于点E,设∠ABC=2α(0°<α<45°).
(1)、试判断直线DE与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.25. 某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.(1)、当销售该纪念品每天能获得利润2160元时,每件的销售价应为多少?(2)、当每件的销售价为多少时,销售该纪念品每天获得的利润最大?并求出最大利润.26. 已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD所在的直线对折,使点B落在点B′处,连结AB',BB',延长CD交BB'于点E,设∠ABC=2α(0°<α<45°). (1)、如图1,若AB=AC,求证:CD=2BE;(2)、如图2,若AB≠AC,试求CD与BE的数量关系(用含α的式子表示);(3)、如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连结EF交BC于点O,设△COE的面积为S1 , △COF的面积为S2 , 求 (用含α的式子表示).27. 已知抛物线 : 是由抛物线 : 平移得到的,并且 的顶点为(1,-4)
(1)、如图1,若AB=AC,求证:CD=2BE;(2)、如图2,若AB≠AC,试求CD与BE的数量关系(用含α的式子表示);(3)、如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连结EF交BC于点O,设△COE的面积为S1 , △COF的面积为S2 , 求 (用含α的式子表示).27. 已知抛物线 : 是由抛物线 : 平移得到的,并且 的顶点为(1,-4) (1)、求 的值;(2)、如图1,抛物线C1与x轴正半轴交于点A,直线 经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.
(1)、求 的值;(2)、如图1,抛物线C1与x轴正半轴交于点A,直线 经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.①若AP=AQ,求点P的坐标;
②若PA=PQ,求点P的横坐标.
(3)、如图2,△MNE的顶点M、N在抛物线C2上,点M在点N右边,两条直线ME、NE与抛物线C2均有唯一公共点,ME、NE均与y轴不平行.若△MNE的面积为16,设M、N两点的横坐标分别为m、n,求m与n的数量关系.