江苏省常州市新北区2020年届九年级下学期调研数学试卷

试卷更新日期：2020-06-09 类型：中考模拟

进入出卷网下载

一、选择题

1. 若∠α=60°，则cosα=（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
2. 在平面直角坐标系xOy中，点A的坐标为（-2，1），则点A关于x轴的对称点的坐标为（）

A、（-2，-1） B、（2，-1） C、（2， 1） D、（-1，2）

查看试题解析
3. 数据2、8、3，5，5，4的众数、中位数分别是（）

A、4.5、5 B、5、4.5 C、5、4 D、5、5

查看试题解析
4. 一次函数y=kx+b的图像经过点（-1，2），则k-b的值是（）

A、-1 B、2 C、1 D、-2

查看试题解析
5. 在平面直角坐标系xOy中，点A的坐标为（1，2），如果射线OA与x轴正半轴的夹角为α，那么sinα的值是（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
6. 如图，从⊙O外一点P引圆的两条切线PA、PB，切点分别是A、B，若∠P=60°，PA=4 $\sqrt{3}$ ，则⊙O的半径长是（）

A、 $\frac{4 \sqrt{3}}{3}$ B、2 C、4 D、2 $\sqrt{3}$

查看试题解析
7. 将一副三角尺如图放置，∠ACB=∠CBD=90°，∠A=30°，∠D=45°，边AB、CD交于O，若OB=1，则OA的长度是（）

A、 $\sqrt{3}$ B、2 C、1 D、 $\frac{\sqrt{3}}{2}$

查看试题解析
8. 如图，在平面直角坐标系xOy中，四边形ABCD是矩形，点A的坐标为（2，0），点B的坐标为（0，4），顶点C在反比例函数y= $\frac{k}{x}$ 的图像上，若 AD：AB=1：2，则k的值是（）

A、8 B、10 C、12 D、6

查看试题解析

二、填空题

9. 若反比例函数y= $\frac{k}{x}$ 的图象经过点A（1，2），则k= ．

查看试题解析
10. 若 $\frac{a}{b} = \frac{1}{2}$ ，则 $\frac{a + b}{b}$ = ．

查看试题解析
11. 学校朗诵比赛，参加决赛的是3名女生和2名男生，现抽签决定比赛顺序，那么第一个出场为女生的概率是.

查看试题解析
12. 如图，△ABC中，点D、E分別在AB、AC上，DE∥BC，AD：DB=1：2，则△ADE与△ABC的面积的比为.

查看试题解析
13. 二次函数y=-x²+4x-3的图象的顶点坐标是.

查看试题解析
14. 学校打算用长16m的篱笆围成一个长方形的生物园饲养小动物，生物园的一面靠墙（如图），面积是30m² ，求生物园的长和宽.设生物园的宽（与墙相邻的一边）为xm，则列出的方程为.

查看试题解析
15. 如图，AB是⊙O的直径，点C、D是圆上位于AB 两侧的点，若∠BAC=58°，则∠D= °.

查看试题解析
16. 已知扇形的面积是 $\frac{2}{3}$ π，圆心角120°，则这个扇形的半径是.

查看试题解析

17. 在研究一次函数y₁=kx+b与反比例函数y₂=

\frac{m}{x}

时，列表如下：

x	…	-2	-1	1	2	3	4	…
y₁=kx+b	…	6	5	3	2	1	0	…
y₂= $\frac{m}{x}$	…	$- \frac{3}{2}$	-3	3	$\frac{3}{2}$	1	$\frac{3}{4}$	…

由此可以推断，当y₁> y₂ ，自变量x的取值范围是.

查看试题解析

18. 如图，在⊙O中，C是弦AB上一点，AC＝2，CB＝4.连接OC，过点C作DC⊥OC，与⊙O交于点D，DC的长为.

查看试题解析

三、解答题

19. 化简：

(1)、 $\frac{\cos 30^{o}}{1 + s i n 30^{o}} + \tan 60^{o}$

(2)、 $\sqrt{{(- 2)}^{2}} - {(\frac{1}{2})}^{- 1} + {(\cos 45^{°})}^{0}$

查看试题解析
20. 解方程：

(1)、x²﹣1＝3（x﹣1）

(2)、x²﹣4x＝－1

查看试题解析
21. 为了解某市初中学生课外阅读情况，调查小组对该市这学期初中学生阅读课外书籍的册数进行了抽样调查，并根据调查结果绘制成如下统计图．
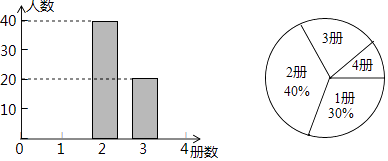
根据统计图提供的信息，解答下列问题：

(1)、本次抽样调查的样本容量是；

(2)、补全条形统计图；

(3)、该市共有12000名初中生，估计该市初中学生这学期课外阅读超过2册的人数．

查看试题解析
22. 一只不透明的袋子中装有4个大小、质地都相同的乒乓球，球面上分别标有数字1、2、3、4.

(1)、搅匀后从中任意摸出1个球，求摸出的乒乓球球面上数字为1的概率；

(2)、搅匀后先从中任意摸出1个球（不放回），再从余下的3个球中任意摸出1个球，求2次摸出的乒乓球球面上数字之和为偶数的概率.

查看试题解析
23. 如图，在△ABC中，BC的垂直平分线分别交BC、AC于点D、E，BE交AD于点F，AB=AD，

(1)、判断△FDB与△ABC是否相似，并说明理由；

(2)、若AF=2，求DF的长.

查看试题解析
24. 如图，在△ABC中，AC=BC，AB⊥x轴，垂足为A.反比例函数y= $\frac{k}{x}$ （x＞0）的图象经过点C，交AB于点D.已知AB=4，BC= $\frac{5}{2}$ .

(1)、若OA=4，求k的值；

(2)、连接OC，若BD=BC，求OC的长.

查看试题解析
25. 如图，已知AB为⊙O的直径，C为⊙O上一点，BG与⊙O相切于点B，交AC的延长线于点D（点D在线段BG上），AC = 8，tan∠BDC = $\frac{4}{3}$

(1)、求⊙O的直径；

(2)、当DG= $\frac{5}{2}$ 时，过G作 $G E // A D$ ，交BA的延长线于点E，说明EG与⊙O相切.

查看试题解析

26. 根据完全平方公式可以作如下推导（a、b都为非负数）

∵ a-2 $\sqrt{a b}$ +b=( $\sqrt{a}$ - $\sqrt{b}$ )²≥0 ∴ a-2 $\sqrt{a b}$ +b≥0

∴ a+b≥2 $\sqrt{a b}$ ∴ $\frac{a + b}{2}$ ≥ $\sqrt{a b}$

其实，这个不等关系可以推广， $\frac{a_{1} + a_{2}}{2}$ ≥ $\sqrt{a_{1} a_{2}}$

$\frac{a_{1} + a_{2} + a_{3}}{3} \geq \sqrt[3]{a_{1} a_{2} a_{3}}$

$\frac{a_{1} + a_{2} + a_{3} + a_{4}}{4} \geq \sqrt[4]{a_{1} a_{2} a_{3} a_{4}}$

… …

$\frac{a_{1} + a_{2} + \dots + a_{n}}{n} \geq \sqrt[n]{a_{1} a_{2} \dots a_{n}}$ （以上a_n都是非负数）

我们把这种关系称为：算术—几何均值不等式

例如：x为非负数时， $x + \frac{1}{x} \geq 2 \sqrt{x \cdot \frac{1}{x}} = 2$ ，则 $x + \frac{1}{x}$ 有最小值.

再如：x为非负数时，x+x+ $\frac{1}{x^{2}} \geq 3 \sqrt[3]{x \cdot x \cdot \frac{1}{x^{2}}} = 3$ .

我们来研究函数： $y = \frac{2}{x} + x^{2}$

(1)、这个函数的自变量x的取值范围是；

(2)、完成表格并在坐标系中画出这个函数的大致图象；

x	…	-3	-2	-1	$\frac{1}{4}$	$\frac{1}{2}$	1	2	3	…
y	…	$8 \frac{1}{3}$	3		$8 \frac{1}{16}$	$4 \frac{1}{4}$		5	$9 \frac{2}{3}$	…

(3)、根据算术—几何均值不等式，该函数在第一象限有最值，是；

(4)、某同学在研究这个函数时提出这样一个结论：当x>a时，y随x增大而增大，则a的取值范围是 .

查看试题解析

27. 如图，一次函数y=kx+b的图象与x轴交于点B（6，0），与y轴交于点A，与二次函数y=ax²的图象在第一象限内交于点C（3，3）.

(1)、求此一次函数与二次函数的表达式；

(2)、若点D在线段AC上，与y轴平行的直线DE与二次函数图象相交于点E，∠ADO=∠OED，求点D坐标.

查看试题解析
28. 二次函数y= $\frac{1}{2}$ (x-h)²+k的顶点在x轴上，其对称轴与直线y=x交于点A（1，1），点P是抛物线上一点，以P为圆心，PA长为半径画圆，⊙P交x轴于B、C两点.

(1)、h= ， k=；

(2)、①当点P在顶点时，BC=▲ ；
②BC的值是否随P点横坐标的变化而变化？如果变化，请说明理由，如果不变化，请求出这个值.

查看试题解析