湖北省武汉市硚口区2020年数学中考模拟试卷(4月)
试卷更新日期:2020-06-09 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、7 B、 C、 D、12. 使 有意义的 的取值范围是( )A、 B、 C、 D、3. 掷一枚质地均匀的硬币10次,下列说法正确的是( )A、每两次必有1次正面向上 B、可能有5次正面向上 C、必有5次正面向上 D、不可能有10次正面向上4. 下列图形中,不是轴对称图的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图是下面哪个图形的俯视图( )
5. 如图是下面哪个图形的俯视图( )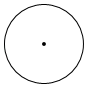 A、
A、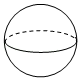 B、
B、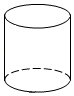 C、
C、 D、
D、 6. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是( )A、 B、 C、 D、7. 我国古代数学名著《孙子算经》中记载了一道题,大意是:有100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?设大马有 匹,小马有y匹,可列方程组为( )A、 B、 C、 D、8. 已知 、 两点在反比例函数 的图象上,下列三个命题:①若 ,则 ;②若 , ,则 ;③过A、B两点的直线与x轴、y轴分别交于C、D两点,连接OA、OB,则 .其中真命题个数是( )A、0 B、1 C、2 D、39. 已知整数 、 、 、 、……满足下列条件: , , , ,……, ( 为正整数)依此类推,则 的值为( )A、 B、 C、 D、10. 如图, 、 是 的切线, 、 为切点, 是劣弧 的中点,连接 并延长交 于 ,若 ,则 的值为( )
6. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是( )A、 B、 C、 D、7. 我国古代数学名著《孙子算经》中记载了一道题,大意是:有100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?设大马有 匹,小马有y匹,可列方程组为( )A、 B、 C、 D、8. 已知 、 两点在反比例函数 的图象上,下列三个命题:①若 ,则 ;②若 , ,则 ;③过A、B两点的直线与x轴、y轴分别交于C、D两点,连接OA、OB,则 .其中真命题个数是( )A、0 B、1 C、2 D、39. 已知整数 、 、 、 、……满足下列条件: , , , ,……, ( 为正整数)依此类推,则 的值为( )A、 B、 C、 D、10. 如图, 、 是 的切线, 、 为切点, 是劣弧 的中点,连接 并延长交 于 ,若 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算 的结果是.12. 自从“新冠病毒”爆发以来,胖胖同学每周且每天3次自测体温.结果统计如下表:
体温(℃)
36.1
36.2
36.3
36.4
36.5
36.6
36.7
次数
2
3
4
6
3
1
2
则这些体温的众数是℃.
13. 计算 的结果是.14. 如图,将菱形纸片 折叠,使点 落在 边的点 处,折痕为 ,若 ,则 的度数是. 15. 二次函数 的图象经过点 , , ,与 轴的负半轴相交,且交点在 的上方.下列四个结论中一定正确的是.
15. 二次函数 的图象经过点 , , ,与 轴的负半轴相交,且交点在 的上方.下列四个结论中一定正确的是.① ;② ;③ ;④ .(填序号即可)
16. (问题探究)如图1, ,直线 ,垂足为 ,交 于点 ,点 到直线 的距离为2,点 到 的距离为1, , ,则 的最小值是;(提示:将线段 沿 方向平移1个单位长度即可解决,如图2所示.)(关联运用)如图3,在等腰 和等腰 中, , 在直线 上, ,连接 、 ,则 的最小值是.

三、解答题
-
17. 计算: .18. 如图,已知AC⊥AE,BD⊥BF,∠1=∠2,求证:AE∥BF.
 19. 2020年2月10日,光明中学团委利用网络平台组织八年级600名学生参加“全民抗疫”知识大赛.为了了解本次大赛的成绩,随机抽取了部分学生的成绩作为样本,按 , , , 四个等级进行统计,制成如下不完整的统计图.
19. 2020年2月10日,光明中学团委利用网络平台组织八年级600名学生参加“全民抗疫”知识大赛.为了了解本次大赛的成绩,随机抽取了部分学生的成绩作为样本,按 , , , 四个等级进行统计,制成如下不完整的统计图.(说明: 级80分-100分, 级70分-79分, 级60-69分, 级0分-59分)

根据所给信息,解答以下问题:
(1)、在扇形统计图中, 级对应的扇形的圆心角是度;(2)、补全条形统计图;(3)、所抽取学生的足球运球测试成绩的中位数会落在等级;(4)、若成绩达到 等级的学生可以选为志愿者,请估计该校八年级600名学生中可以选为志愿者学生有多少人?20. 请仅用无刻度直尺完成下列画图,不写画法,保留画图痕迹. (1)、如图1,在 的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点. 的顶点在格点上,过点 画一条直线平分 的面积;(2)、如图2,点 在正方形 的内部,且 ,过点 画一条射线平分 ;(3)、如图3,点 、 、 均在 上,且 ,在优弧 上画 、 两点,使 .21. 在等边 中,点 在边 上,以 为半径的 交 于点 ,过点 作 于点 .
(1)、如图1,在 的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点. 的顶点在格点上,过点 画一条直线平分 的面积;(2)、如图2,点 在正方形 的内部,且 ,过点 画一条射线平分 ;(3)、如图3,点 、 、 均在 上,且 ,在优弧 上画 、 两点,使 .21. 在等边 中,点 在边 上,以 为半径的 交 于点 ,过点 作 于点 . (1)、如图1,求证: 为 的切线;(2)、如图2,连接 交 于点 ,若 为 中点,求 的值.22. 某超市销售一种文具,进价为 5(元/件),售价为6(元/件)时,当天的销售量为100件,在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件,设当天销售单价统一为 (元/件)( ,且 是按0.5元的倍数上涨),当天销售利润为 元.(1)、求 与 的函数关系式(不要求写出自变量的取值范围);(2)、要使当天销售利润不低于240元,求当天销售单价的范围;(3)、若每件文具的利润不超过60%,要使当天获得利润最大,每件文具售价为多少元?并求出最大利润.23. 在 中, ,点 在底边 上, 的两边分别交 、 所在直线于 、 两点, , .(1)、如图1,若 , ,求证: ;
(1)、如图1,求证: 为 的切线;(2)、如图2,连接 交 于点 ,若 为 中点,求 的值.22. 某超市销售一种文具,进价为 5(元/件),售价为6(元/件)时,当天的销售量为100件,在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件,设当天销售单价统一为 (元/件)( ,且 是按0.5元的倍数上涨),当天销售利润为 元.(1)、求 与 的函数关系式(不要求写出自变量的取值范围);(2)、要使当天销售利润不低于240元,求当天销售单价的范围;(3)、若每件文具的利润不超过60%,要使当天获得利润最大,每件文具售价为多少元?并求出最大利润.23. 在 中, ,点 在底边 上, 的两边分别交 、 所在直线于 、 两点, , .(1)、如图1,若 , ,求证: ; (2)、如图2,求 的值(含 的式子表示);
(2)、如图2,求 的值(含 的式子表示); (3)、如图3,连接 ,若 , ,且 ,直接写出 的值为.
(3)、如图3,连接 ,若 , ,且 ,直接写出 的值为. 24. 抛物线 : 与 轴交于点 、 两点,与 轴交于点 ,且 .(1)、直接写出抛物线 的解析式;(2)、如图1,点 在 轴左侧的抛物线 上,将点 先向右平移4个单位长度,再向下平移 个单位长度,得到的对应点 恰好落在抛物线 上,若 ,求点 的坐标;
24. 抛物线 : 与 轴交于点 、 两点,与 轴交于点 ,且 .(1)、直接写出抛物线 的解析式;(2)、如图1,点 在 轴左侧的抛物线 上,将点 先向右平移4个单位长度,再向下平移 个单位长度,得到的对应点 恰好落在抛物线 上,若 ,求点 的坐标; (3)、如图2,将抛物线 向上平移2个单位长度得到抛物线 ,一次函数 的图象 与抛物线 只有一个公共点 ,与 轴交于点 ,探究: 轴上是否存在定点 满足 ?若存在,求出点 的坐标;否则,说明理由.
(3)、如图2,将抛物线 向上平移2个单位长度得到抛物线 ,一次函数 的图象 与抛物线 只有一个公共点 ,与 轴交于点 ,探究: 轴上是否存在定点 满足 ?若存在,求出点 的坐标;否则,说明理由.