浙江省杭州市拱墅区、滨江区、余杭区、下沙开发区、钱塘新区2020年数学中考一模试卷

试卷更新日期：2020-06-09 类型：中考模拟

进入出卷网下载

一、选择题：本大题有10个小题，毎小题3分，共30分.

1. 计算下列各式，结果为负数的是（）

A、(-7)÷(-8) B、(-7)×(-8) C、(-7)-(-8) D、(-7)+(-8)

查看试题解析
2. 世界上最深的海沟是太平洋的马里亚纳海沟，海拔为-11034米，数据-11034用科学记数法表示为（）

A、1.1034×10⁴ B、-1.1034⁴ C、-1.1034×10⁴ D、-1.1034×10⁵

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{{(- 7)}^{2}}$ =±7 B、 $\sqrt{{(- 7)}^{2}}$ =-7 C、 $\sqrt{1 \frac{1}{4}}$ =1 $\frac{1}{2}$ D、 $\sqrt{1 \frac{1}{4}}$ = $\frac{\sqrt{5}}{2}$

查看试题解析
4. 如图，测得一商场自动扶梯的长为l，自动扶梯与地面所成的角为θ，则该自动扶梯到达的高度h为（）

A、l·sinθ B、 $\frac{l}{\sin θ}$ C、l·cosθ D、 $\frac{l}{\cos θ}$

查看试题解析
5. 某汽车队运送一批救灾物资，若每辆车装4吨，还剩下8吨未装；若每辆车装4.5吨，恰好装完.设这个车队有x辆车，则（）

A、4(x+8)=4.5x B、4x+8=4.5x C、4.5(x-8)=4x D、4x+4.5x=8

查看试题解析
6. 一次中学生田径运动会上，21名参加男子跳高项目的运动员成绩統计如下：

成绩（m）

1.50

1.55

1.60

1.65

1.70

人数

■

8

6

■

1

其中有两个数据被雨水淋混模不清了，则在这组数据中能确定的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. 如图，AB∥CD∥MN，点M，N分别在线段AD，BC上，AC与MN交于点E．则（）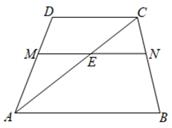

A、 $\frac{D M}{A E} = \frac{C E}{A M}$ B、 $\frac{A M}{C N} = \frac{B N}{D M}$ C、 $\frac{D C}{M E} = \frac{A B}{E N}$ D、 $\frac{A E}{A M} = \frac{C E}{D M}$

查看试题解析
8. 如图，AB//CD，点E是直线AB上的点，过点E的直线 $l$ 交直线CD于点F，EG平分 $∠ B E F$ 交CD于点G，在直线 $l$ 绕点E旋转的过程中，图中 $∠ 1$ ， $∠ 2$ 的度数可以分别是（）

A、 $30^{°}$ ， $110^{°}$ B、 $56^{°}$ ， $70^{°}$ C、 $70^{°}$ ， $40^{°}$ D、 $100^{°}$ ， $40^{°}$

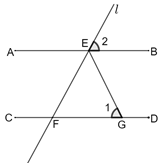查看试题解析
9. 如图所示，正方形ABCD中，E为BC边上一点，连接AE，作AE的垂直平分线交AB于G，交CD于F，若BG＝2BE，则DF：CF的长为（）

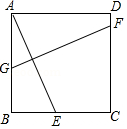A、 $\frac{\sqrt{5} - 1}{3}$ B、 $\frac{\sqrt{5} + 1}{8}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2}{5}$

查看试题解析
10. 已知二次函数y=ax²+2ax+3a-2（a是常数，且a≠0）的图象过点M（x₁ ， -1），N（x₂ ， -1），若MN的长不小于2，则a的取值范围是（）

A、a≥ $\frac{1}{3}$ B、0<a≤ $\frac{1}{3}$ C、- $\frac{1}{3}$ ≤a<0 D、a≤- $\frac{1}{3}$

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分

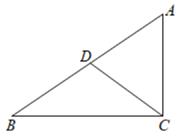
11. 因式分解x²-4=。

查看试题解析
12. 如图，在△ABC中，∠ACB=90°，CD是△ABC的中线，若∠DCB=40°，则∠A的度数为 °．

查看试题解析
13. 同时抛掷两枚质地均匀的硬币，两枚硬币全部正面向上的概率是.

查看试题解析
14. 如图，圆弧形弯道两边的直道在连接点处与弯道相切，测得∠AEB=120°，圆弧的半径是2千米，则该段圆弧形弯道的长为千米（结果保留π）

查看试题解析
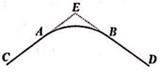15. 某函数满足当自变量x=-1时，函数的值y=2，且函数y的值始终随自变量x的增大而减小，写出一个满足条件的函数表达式．

查看试题解析
16. 如图，在等边三角形ABC的AC，BC边上各取一点P，Q，使AP=CQ，AQ，BP相交于点O．若BO=6，PO=2，则AP的， AO的长为．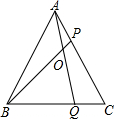

查看试题解析

三、解答题：本大题有7个小题，共66分．

17. 计算：

(1)、（a-3）（a+1）-（a-3）²

(2)、 $\frac{4}{a^{2} - 4} + \frac{1}{a + 2}$

查看试题解析
18. 根据《N家学生体质健康标准》规定：九年级男生坐位体前屈达到17.8厘米及以上为优秀；达到13.8厘米至17.7厘米为良好；达到-0.2厘米至13.7厘米为及格；达到-0.3厘米及以下为不及格，某校为了了解九年级男生的身体柔韧性情况，从该校九年级男生中随机抽取了20%的学生进行坐位体前屈测试，并把测试结果绘制成如图所示的统计表和扇形统计图（部分信息不完整），请根据所给信息解答下列问题．

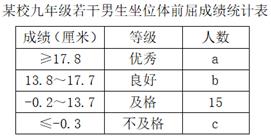
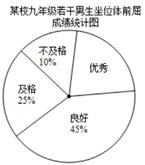(1)、求参加本次坐位体前屈测试的人数；

(2)、求a，b，c的值；

(3)、试估计该年级男生中坐位体前屈成绩不低于13.8厘米的人数．

查看试题解析
19. 如图，在△ABC中，AB<AC<BC，以点A为圆心，线段AB的长为半径画弧，与BC边交于点D，连接AD过点D作DE⊥AD，交AC于点E．

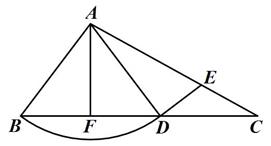(1)、若∠B=50°，∠C=28°，求∠AED度数；

(2)、若点F是BD的中点，连接AF，求证：∠BAF=∠EDC．

查看试题解析
20. 某游泳池毎次换水前后水的体积基本保持不变，当该游泳池以每小时300立方米的速度放水时，经3小时能将池内的水放完．设放水的速度为x立方米/时，将池内的水放完需y小时．已知该游泳池毎小时的最大放水速度为350立方米

(1)、求y关于x的函数表达式．

(2)、若该游泳池将放水速度控制在每小时200立方米至250立方米（含200立方米和250立方米），求放水时间y的范围．

(3)、该游泳池能否在2.5小时内将池内的水放完？请说明理由．

查看试题解析
21. 已知：⊙O的两条弦AB，CD相交于点M，且AB=CD．

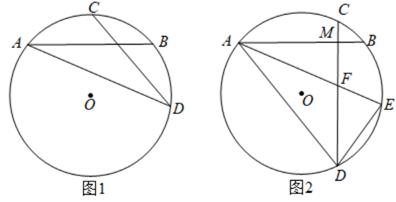(1)、如图1，连接AD．求证：AM=DM．

(2)、如图2，若AB⊥CD，在弧BD上取一点E，使弧BE=弧BC，AE交CD于点F，连AD、DE．
①利断∠E与∠DFE是否相等，并说明理由．

②若DE=7，AM+MF=17，求△ADF的面积．

查看试题解析
22. 设二次函数y=（ax-1）（x-a），其中a是常数，且a≠0．

(1)、当a=2时，试判断点（- $\frac{1}{2}$ ，-5）是否在该函数图象上．

(2)、若函数的图象经过点（1，-4），求该函数的表达式．

(3)、当 $\frac{a}{2}$ -1≤x≤ $\frac{a}{2}$ +1时，y随x的增大而减小，求a的取值范围．

查看试题解析
23. 如图1，折叠矩形纸片ABCD，具体操作：①点E为AD边上一点（不与点A，D重合），把△ABE沿BE所在的直线折叠，A点的对称点为F点；②过点E对折∠DEF，折痕EG所在的直线交DC于点G，D点的对称点为H点．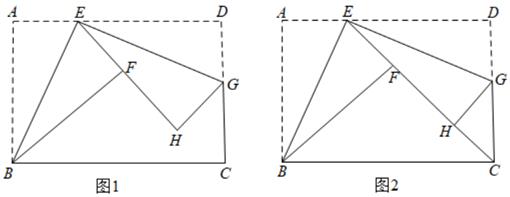

(1)、求证：△ABE∽△DEG．

(2)、若AB=3，BC=5
①点E在移动的过程中，求DG的最大值

②如图2，若点C恰在直线EF上，连接DH，求线段DH的长．

查看试题解析

成绩（m）	1.50	1.55	1.60	1.65	1.70
人数	■	8	6	■	1