浙江省湖州市吴兴区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-06-09 类型：期中考试

进入出卷网下载

一、选择题

1. 下列四个方程中是二元一次方程的为（）

A、4x﹣1＝x B、 $x + \frac{1}{x} = 2$ C、2x﹣3y＝2 D、xy＝9

查看试题解析
2. 计算a³÷a正确的结果是（）

A、2a³ B、2a C、a² D、a³

查看试题解析
3. 某种冠状病毒的大小约为0.000125mm，该数用科学记数法表示正确的是（）

A、0.125×10^﹣3 B、0.125×10^﹣4 C、1.25×10^﹣3 D、1.25×10^﹣4

查看试题解析
4. 在同一平面内，若三条直线 $a, b, c$ 同时满足 $a ⊥ b, b ⊥ c,$ 则 $a 与 c$ 的关系是（）

A、平行 B、垂直 C、相交 D、垂直或平行

查看试题解析
5. 下列哪一组不是二元一次方程 $3 x + y = 10$ 的解（）

A、 ${\begin{cases} x = 1 \\ y = 7 \end{cases}$ B、 ${\begin{cases} x = 2 \\ y = 3 \end{cases}$ C、 ${\begin{cases} x = 2 \\ y = 4 \end{cases}$ D、 ${\begin{cases} x = 3 \\ y = 1 \end{cases}$

查看试题解析
6. 下列多项式哪一项可以用平方差公式分解因式（）

A、 $4 x^{2} + y^{2}$ B、 $a^{2} + 3$ C、 $y^{2} - 4 x^{2}$ D、 $-4 x^{2} - y^{2}$

查看试题解析
7. 如图是一块断尺，一块等腰直角三角板的直角顶点刚好落在断尺的下端.则下列结论中，不正确的是（）

A、∠1+∠3＝90° B、∠5﹣∠2＝90° C、∠2+∠3+∠4+∠5＝270° D、∠5﹣∠3＝90°

查看试题解析
8. 已知a﹣b＝4，则a²﹣b²﹣8b+1的值为（）

A、4 B、15 C、17 D、19

查看试题解析
9. 如图，两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起，固定三角形ABC不动，将三角形DEF向右平移，当点E和点C重合时，停止移动，设DE交AC于G.给出下列结论：①四边形ABEG的面积与CGDF的面积相等；②AD∥EC，且AD＝EC；③若BF=8cm，EC=2cm，那么三角形DEF向右平移了2cm，则上述说法正确的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“友好数”如（ $8 = 3^{2} - 1^{2}, 16 = 5^{2} - 3^{2}$ ，即8,16均为“友好数”），在不超过2020的正整数中，所有的“友好数”之和为（）

A、255054 B、255064 C、250554 D、255024

查看试题解析

二、填空题

11. 因式分解： $a^{2} - a$ = ．

查看试题解析
12. 已知方程 $\frac{1}{2} x + y = 11$ ，用含x的代数式表示y，那么y＝.

查看试题解析
13. 若多项式 $x^{2} + a x - 2$ 可以因式分解为 $(x - 1) (x + b)$ ，则 $a + 2b$ 的值为.

查看试题解析
14. 如图，将一块长方形纸条折成如图的形状，若已知∠1=70°，则∠2的度数为.

查看试题解析
15. 已知： $2 x + 3 y - 3 = 0, 则 4^{x} \times 8^{y} =$ .

查看试题解析
16. 在边长为 $a$ 的正方形中，放入两张边长为 $b$ 的正方形纸片( $a > b$ )，如图①所示，阴影部分面积记为 $S_{1}$ ；若放入三张边长为 $b$ 的正方形纸片，如图②所示，阴影部分面积和记为 $S_{2}$ .若 $\frac{S_{1}}{S_{2}} = 4$ ，则 $a 与 b$ 的数量关系为.

查看试题解析

三、解答题：

17.

(1)、计算题 ${-3}^{2} + （ π -3 ）^{0} + {(\frac{1}{3})}^{-2}$ .

(2)、解方程组： ${\begin{cases} 4x - 3 y - 10 = 0 \\ 3 x - 2 y = 0 \end{cases}$ .

查看试题解析
18. 先化简，再求值： $[{(x - y)}^{2} + y (2 x - y)] \div (\frac{1}{2} x)$ ,其中 $x = 1, y = \frac{1}{2}$ .

查看试题解析
19. 如图，∠AFD＝∠1，AC∥DE.

(1)、试说明：DF∥BC；

(2)、若∠1＝66°，DF平分∠ADE，求∠B的度数.

查看试题解析
20. 若 $| a + b - 5 | + {(a b - 3)}^{2} = 0$

(1)、求 $a^{2} + b^{2}$ 的值；

(2)、求 $- a^{3} b - 2 a^{2} b^{2} - a b^{3}$ 的值.

查看试题解析
21. 两位同学将一个二次三项式分解因式，一位同学因看错了一次项系数而分解成 $2 (x - 1) (x - 9)$ ，另一位同学因看错了常数项而分解成 $2 (x - 2) (x - 4)$ ，请将原多项式分解因式.

查看试题解析
22. 如图，某小区将长方形花坛ABCD进行升级改造，修建横向、纵向各一条小路，阴影部分种植草坪.已知，BC=3x米，AB=2x米，EF=y米，GH=2y米.

(1)、用含x、y的代数式表示草坪（阴影）部分的面积；

(2)、若x=3y=6米，每平方米草坪的造价为100元，则修建草坪需花费多少钱？

查看试题解析
23. 如图1是某机场的平地电梯，电梯AB的长度为120米，如图2所示.若两人不乘电梯在地面匀速行走，小明每分钟的路程是小王的1.5倍，且1.5分钟后，小明比小王多行走30米.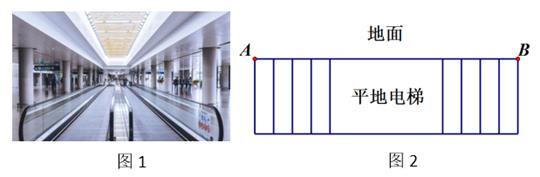

(1)、求两人在地面上每分钟各行走多少米？

(2)、若两人在平地电梯上行走，电梯向前行驶，两人也同时在电梯上行走.当小明到达B处时，小王还剩 $\frac{80}{3}$ 米.
①求平地电梯每分钟行驶多少米？

②当小明到达B处时，发现有一袋行李忘在A处，同时关注此时为7点55分，小明马上从地面返回A处，拿了行李后立即乘平地电梯（同时行走）去B处.问小明能否在8点前和小王汇合，并说明理由.

查看试题解析
24. 某市为了美化亮化某景点，在两条笔直的景观道MN、QP上，分别放置了A、B两盏激光灯，如图所示，A灯发出的光束自AM逆时针旋转至AN便立即回转；B灯发出的光束自BP逆时针旋转至BQ便立即回转，两灯不间断照射，A灯每秒转动a度，B灯每秒转动b度，且满足 $3^{- b} = \frac{1}{3} ， 2^{3 b - a} = 1$ ，若这两条景观道的道路是平行的，即MN∥QP.

(1)、求a、b的值；

(2)、若B灯先转动10秒，A灯才开始转动：
当A灯转动5秒时，两灯的光束AM′和BP′到达如图①所示的位置，试问AM′和BP′是否平行？请说明理由；

(3)、当B灯光束第一次达到BQ之前，两灯的光束是否能互相垂直，如果能互相垂直，那么此时A灯旋转的时间为秒.（不要求写出解答过程）

查看试题解析