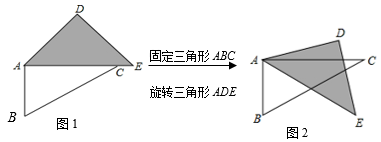
浙江省宁波市奉化区锦屏协作区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-06-09 类型：期中考试

进入出卷网下载

一、选择题

1. 如图，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是（）

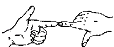A、同位角 B、内错角 C、对顶角 D、同旁内角

查看试题解析
2. 下列方程中，是二元一次方程的是（）

A、 $x + 2 y = 5$ B、 $x y = 3$ C、 $3 x + y^{2} = 5$ D、 $\frac{1}{x} + y = 1$

查看试题解析
3. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微笑的无花果,质量只有0.000000076克,将0.000000076科学记数法表示为（）

A、 $7.6 \times 10^{- 8}$ B、 $7.6 \times 10^{- 9}$ C、 $7.6 \times 10^{8}$ D、 $7.6 \times 10^{9}$

查看试题解析
4. 下列计算结果正确的是（）

A、a³×a⁴＝a¹² B、a⁵÷a＝a⁵ C、（ab²）³＝ab⁶ D、（a³）²＝a⁶

查看试题解析
5. 下列从左边到右边的变形，属于因式分解的是（）

A、（x+1）（x-1）＝x²-1 B、x²-2x+1＝x（x-2）+1 C、a（x-y）=ax-ay D、x²+2x+1＝（x+1）²

查看试题解析
6. 计算：（8x³﹣12x²﹣4x）÷（﹣4x）＝（）

A、﹣2x²+3x B、﹣2x²+3x+1 C、﹣2x²+3x﹣1 D、2x²+3x+1

查看试题解析
7. 如图，下列能判定 $A B ∥ C D$ 的条件有（）个.
（1）∠B+∠BCD=180°；（2）∠1=∠2；（3）∠3=∠4；（4）∠B=∠5.

A、1 B、2 C、3 D、4

查看试题解析
8. 若多项式 $x^{2} + k x + 9$ 是一个完全平方式，则常数 $k$ 的值是（）

A、6 B、3 C、 $\pm 6$ D、 $\pm 3$

查看试题解析
9. 如果x+m与x+8的乘积中不含x的一次项，则m的值是（）

A、 $-$ 8 B、8 C、0 D、1

查看试题解析
10. 为了奖励疫情期间线上学习表现优异的同学，某校决定用1200元购买篮球和排球，其中篮球每个120元，排球每个90元，在两种球类都购买且资金恰好用尽的情况下，购买方案有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
11. 如图1，∠DEF＝25°，将长方形纸片ABCD沿直线EF折叠成图2，再沿折痕GF折叠成图3，则∠CFE的度数为（）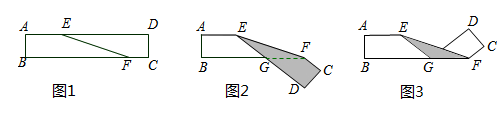

A、105° B、115° C、130° D、155°

查看试题解析
12. 已知（m $-$ 2018）²+（m $-$ 2020）² $=$ 34，则（m $-$ 2019）²的值为（）

A、4 B、8 C、12 D、16

查看试题解析

二、填空题

13. 因式分解 $a x^{2} - a x$ =.

查看试题解析
14. 化简： $(2 x - y) (x - 3 y) =$ .

查看试题解析
15. 若 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是方程ax+y＝3的解，则a＝.

查看试题解析
16. 若a+m=200，a $-$ m=4，则a² $-$ m² =.

查看试题解析
17. 计划在一块长为10米，宽为7米的长方形草坪上，修建一条宽为2米的人行道，则剩余草坪的面积为平方米.

查看试题解析
18. 如图所示为正方形的房屋结构平面图，其中主卧与客卧都是正方形，其面积之和比其余面积（阴影部分）多 $9 m^{2}$ ，则主卧和客卧的周长之差为 $m$ .

查看试题解析

三、解答题

19. 计算：

(1)、 $（ - 1 ）^{2020} - {(π + 1)}^{0} + 3^{- 1}$

(2)、 ${(a^{2})}^{4} \div a^{2}$

查看试题解析
20. 解方程组：

(1)、 ${\begin{matrix} 2 x + 3 y = 1 \\ x = 5 + 3 y \end{matrix}$

(2)、 ${\begin{matrix} 2 x + y = 1 \\ 3 x - 2 y = 12 \end{matrix}$

查看试题解析
21. 先化简，再求值：已知x = $-$ 5，求 $（ x + 1 ）^{2} - （ x + 3 ）（ x - 3 ）$ 的值.

查看试题解析
22. 如图，已知BE平分∠ABC，点D在射线BA上，且∠ABE=∠BED .

(1)、判断BC与DE的位置关系，并说明理由 .

(2)、当∠ABE=25°时，求∠ADE的度数 .

查看试题解析
23. 疫情无情人有情，八方相助暖人心.一爱心人士向某社区捐赠了A品牌一次性医用口罩5000个和B品牌免洗消毒液100瓶，总价值18000元.已知10个A品牌一次性医用口罩与1瓶B品牌免洗消毒液共需84元.求A品牌一次性医用口罩和B品牌免洗消毒液的单价分别是多少？

查看试题解析
24. 一天，小聪和小慧玩纸片拼图游戏，发现利用图①中的三种纸片各若干可以拼出一些长方形来解释某些等式，比如图②可以解释为：（a+2b）（a+b）＝a²+3ab+2b²

(1)、图③可以解释为等式：.

(2)、要拼出一个长为a+3b，宽为2a+b的长方形，需要如图所示的块，块，块；

(3)、如图④，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个小长方形的两边长（x＞y），观察图形，以下关系式正确的是（填序号）.
① x+y＝m；② x²﹣y²＝mn；③ 4xy $= m^{2} - n^{2} ；$ ④ x²+y²＝ $\frac{m^{2} + n^{2}}{2}$ .

查看试题解析
25. 如图，已知AM∥BN，∠A=58°，点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D.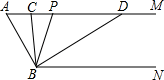

(1)、①∠ABN的度数是度；②∵AM∥BN，∴∠ACB=∠.

(2)、求∠CBD的度数.

(3)、当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律.

(4)、当点P运动到使∠ACB=∠ABD时，∠ABC的度数是（直接写出结果）

查看试题解析
26. 因式分解： $（ 3 x + y ）^{2} - (x - 3 y) (3 x + y) =$ .

查看试题解析
27. 已知 ${\begin{matrix} x + 7 y + 11 z = 9 \\ 2 x + 5 y + 4 z = 15 \end{matrix}$ ，则 $x + y - z =$ .

查看试题解析
28. 已知实数a，b，c满足 $2^{a} = 5 ， 2^{b} = 10 ， 2^{c} = 80 ，$ 则 $2019 a - 4039 b + 2020 c$ 的值为 .

查看试题解析
29. 如图1，已知三角形ABC与三角形ADE摆放在一起，点A、C、E在同一直线上，其中∠ACB＝30°，∠DAE＝45°，∠BAC＝∠D＝90°.如图2，固定三角形ABC，将三角形ADE绕点A按顺时针方向旋转，记旋转角∠CAE＝α（0°＜α＜180°）.

(1)、当α为度时，AD∥BC；

(2)、在旋转过程中，试探究∠CAD与∠BAE之间的关系；

(3)、当三角形ADE的一边与三角形ABC的某一边平行（不共线）时，直接写出旋转角α所有可能的度数（第（1）题的结论除外）.

查看试题解析