江苏省无锡经开区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-06-09 类型：期中考试

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、a＋2a＝3a² B、a³·a²＝a⁵ C、(a⁴)²＝a⁶ D、a³＋a⁴＝a⁷

查看试题解析
2. “碧玉妆成一树高，万条垂下绿丝绦”. 每到春天，人们流连于柳绿桃红之间的同时也被漫天飞舞的柳絮所烦扰.据测定，柳絮纤维的直径约为0.0000105m，该数值用科学记数法表示为（）

A、1.05×10⁵ B、1.05×10^－5 C、－1.05×10⁵ D、105×10^－7

查看试题解析
3. 下列整式乘法中，能运用平方差公式进行运算的是（）

A、(2a＋b)(2b－a) B、(m＋b)(m－b) C、(a－b)(b－a) D、(－x－b)(x＋b)

查看试题解析
4. 如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（）

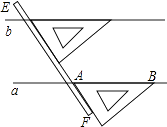A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
5. 一个多边形的内角和是900°，这个多边形的边数是（）

A、10 B、9 C、8 D、7

查看试题解析
6. 如图，将△ABC沿BC方向平移3cm得到△DEF，若△ABC的周长为20cm，则四边形ABFD的周长为（）

A、20cm B、22cm C、24cm D、26cm

查看试题解析
7. 如图，将一个含有45°角的直角三角尺放在两条平行线m、n上，已知∠α=120°，则∠β的度数是（）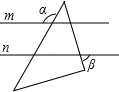

A、45° B、60° C、65° D、75°

查看试题解析
8. 有5根小木棒，长度分别为2cm、3cm、4cm、5cm、6cm，任意取其中的3根小木棒首尾相接搭三角形，可搭出不同的三角形的个数为（）

A、5个 B、6个 C、7个 D、8个

查看试题解析
9. 比较2⁵⁵、3⁴⁴、4³³的大小（）

A、2⁵⁵＜3⁴⁴＜4³³ B、4³³＜3⁴⁴＜2⁵⁵ C、2⁵⁵＜4³³＜3⁴⁴ D、3⁴⁴＜4³³＜2⁵⁵

查看试题解析
10. 在数学中，为了书写简便，18世纪数学家欧拉就引进了求和符号“ $\sum_{}^{}$ ”.如记 $\sum_{k = 1}^{n} k$ =1+2+3+…+（n﹣1）+n， $\sum_{k = 3}^{n} (x + k)$ =（x+3）+（x+4）+…+（x+n）；已知 $\sum_{k = 3}^{n} [(x + k) (x - k + 1)] = 3 x^{2} + 3 x + m$ ，则m的值是（）

A、﹣62 B、﹣38 C、﹣40 D、﹣20

查看试题解析

二、填空题

11. 若a^m=5，aⁿ=3，则a^m+n=.

查看试题解析
12. 已知x²＋x＝2020，则代数式(x＋2)(x－1)的值为.

查看试题解析
13. 如图，已知AB∥CD，∠1=130°，则∠2=.

查看试题解析
14. 把一副常用的三角尺按如图所示的方式拼在一起，则 $∠ A B C$ =°

查看试题解析
15. 若 $2 a + b = - 3 ， 2 a - b = 2$ ，则 $4 a^{2} - b^{2} =$ .

查看试题解析
16. 若多项式a²－（k－2）a＋4是完全平方式，则k的值为.

查看试题解析
17. 如图，若干全等正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需个五边形．

查看试题解析
18. 如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为4、5、7，四边形DHOG面积为.

查看试题解析

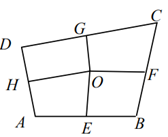
三、解答题

19. 计算或化简：

(1)、(－1)²⁰²¹－2^-1+(π－3.14)⁰；

(2)、(x+2)²－x(x－3)；

(3)、a⁸÷a²-(-3a²)³

(4)、(a－b) (a＋b)－(a－2b) ².

查看试题解析
20. 先化简，再求值：4（x﹣1）²﹣（2x+3）（2x﹣3），其中x＝﹣1．

查看试题解析
21. 画图并填空：如图，方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点D的对应点D′.

(1)、①根据特征画出平移后的△A′B′C′；
②利用网格的特征，画出AC边上的高BE；

(2)、若连接AA′，CC′，则这两条线段之间的关系是.

查看试题解析
22. 如图，BE是△ABC的角平分线，DE∥BC，交AB于点D，∠A=126°，∠DEB=14°，求∠BEC的度数.

查看试题解析
23.

(1)、计算：(x－1)(x²＋x＋1)=；
(2x－3)(4x²＋6x＋9)=；

(3x－4y)(9x²＋12xy＋16y²)=；

归纳：(a－b)()=；

(2)、应用：27m³－125n³= ()()

查看试题解析
24. 如图， AE、 DE、 BF、 CF 分别是四边形 ABCD（四边不相等）的内角角平分线，AE、 BF 交于点 G， DE、 CF 交于点 H.

(1)、探索∠FGE 与∠FHE 有怎样的数量关系，并说明理由.

(2)、∠FGE 与∠FHE 有没有可能相等？若相等，则四边形 ABCD 的边有何结论？请说明理由.

查看试题解析
25.

(1)、教材在探索平方差公式时利用了面积法，面积法可以帮助我们直观地推导或验证公式，俗称“无字证明”，例如，著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为a，较小的直角边长都为b，斜边长都为c），大正方形的面积可以表示为c² ，也可以表示为4× $\frac{1}{2}$ ab＋(a－b)² ，所以4× $\frac{1}{2}$ ab＋(a－b)²=c² ，即a²＋b²=c².由此推导出重要的勾股定理：如果直角三角形两条直角边长为a，b，斜边长为c，则a²＋b²=c².图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理.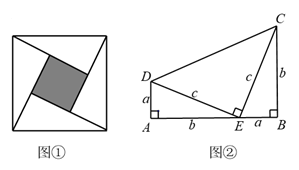

(2)、试用勾股定理解决以下问题：
如果直角三角形ABC的两直角边长为3和4，则斜边上的高为.

(3)、试构造一个图形，使它的面积能够解释(a－2b)²=a²－4ab＋4b² ，画在上面的网格中，并标出字母a，b所表示的线段.

查看试题解析
26. 如图

(1)、光线从空气中射入水中会产生折射现象，同时光线从水中射入空气中也会产生折射现象，如图1，光线a从空气中射入水中，再从水中射入空气中，形成光线b，根据光学知识有∠1＝∠2，∠3＝∠4，请判断光线a与光线b是否平行，并说明理由.

(2)、光线照射到镜面会产生反射现象，由光学知识，入射光线与镜面的夹角与反射光线与镜面的夹角相等，如图2有一口井，已知入射光线a与水平线OC的夹角为36°，问如何放置平面镜MN，可使反射光线b正好垂直照射到井底？（即求MN与水平线的夹角）

(3)、如图3，直线EF上有两点A、C，分别引两条射线AB、CD.∠BAF＝110°，∠DCF＝50°，射线AB、CD分别绕A点，C点以1度/秒和3度/秒的速度同时顺时针转动，设时间为t，在射线CD转动一周的时间内，当t= ，使得CD与AB平行.

查看试题解析