湖北省武汉市武昌区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-06-09 类型：期中考试

进入出卷网下载

一、选择题

1. 下列哪些图形是通过平移可以得到的（）

A、 B、 C、 D、

查看试题解析
2. 点P(-1，5)所在的象限是（）

A、第一象限　 B、第二象限　　 C、第三象限　　 D、第四象限

查看试题解析
3. $\sqrt{38}$ 在下面哪两个整数之间（）

A、5和6 B、6和7 C、7和8 D、8和9

查看试题解析
4. 下列能判断AB∥CD的是（）

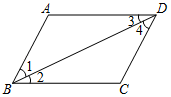A、∠1＝∠4 B、∠2＝∠3 C、∠A＝∠C D、∠A+∠ABC＝180°

查看试题解析
5. 16的平方根是（）

A、2 B、 $\pm 2$ C、4 D、 $\pm 4$

查看试题解析
6. 若 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是方程组 ${\begin{array}{l} x + y = 3 \\ 2 x + a y = 6 \end{array}$ 的解，则a值为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 甲、乙二人同时同地出发，都以不变的速度在环形路上奔跑.若反向而行，每隔3min相遇一次，若同向而行，则每隔6min相遇一次，已知甲比乙跑得快，设甲每分钟跑x圈，乙每分钟跑y圈，则可列方程为（）

A、 ${\begin{array}{l} x - y = 3 \\ x + y = 6 \end{array}$ B、 ${\begin{array}{l} x + y = 3 \\ x - y = 6 \end{array}$ C、 ${\begin{array}{l} 3 x + 3 y = 1 \\ 6 x - 6 y = 1 \end{array}$ D、 ${\begin{array}{l} 3 x - 3 y = 1 \\ 6 x + 6 y = 1 \end{array}$

查看试题解析
8. 如图，O在直线AB上，OC平分∠DOA（大于90°），OE平分∠DOB，OF⊥AB，则图中互余的角有（）对.

A、6 B、7 C、8 D、9

查看试题解析
9. 如图，在平面直角坐标系上有点A(1，0)，点A第一次跳动至点A₁(﹣1，1)，第二次向右跳动3个单位至点A₂(2，1)，第三次跳动至点A₃(﹣2，2)，第四次向右跳动5个单位至点A₄(3，2)，…，以此规律跳动下去，点A第2020次跳动至点A₂₀₂₀的坐标是（）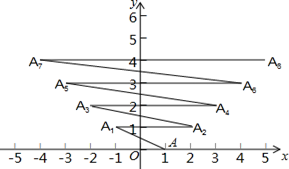

A、(1012，1011) B、(1009，1008) C、(1010，1009) D、(1011，1010)

查看试题解析
10. 如图，AB∥CD，点E为AB上方一点，FB，HG分别为∠EFG，∠EHD的角平分线，若∠E+2∠G＝150°，则∠EFG的度数为（）

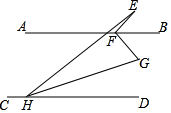A、90° B、95° C、100° D、150°

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{64}$ = ．

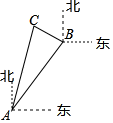
查看试题解析
12. 如图，已知点B在点A的北偏东32°，点C在点B的北偏西58°，CB＝12，AB＝9，AC＝15，则△ABC的面积为.

查看试题解析
13. 若点P在第三象限，且点P到x，y轴的距离分别为3，2，则点P的坐标为.

查看试题解析
14. 如图，将一张纸片沿EF进行折叠，已知AB∥CD，若∠DFC′＝50°，则∠AEF＝.

查看试题解析
15. 若∠A的两边与∠B的两边分别平行，∠A比∠B的3倍小60°，则∠B＝.

查看试题解析
16. 已知关于x，y的二元一次方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解为 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ ，则关于x，y的方程组 ${\begin{array}{l} 3 a_{1} x - b_{1} y = 4 c_{1} \\ 3 a_{2} x - b_{2} y = 4 c_{2} \end{array}$ 的解为.

查看试题解析

三、解答题

17. 计算

(1)、 $\sqrt{\frac{1}{4}} + \sqrt{25}$ ﹣ $\sqrt[3]{\frac{1}{8}}$

(2)、 $\sqrt{2}$ （ $\sqrt{2} + 2$ ）﹣ $\sqrt{2}$

查看试题解析
18. 解下列方程

(1)、（x+2）²＝9

(2)、 ${\begin{array}{l} 3 x + 2 y = 8 \\ x - y = 1 \end{array}$

查看试题解析
19. 阅读下列文字，并完成证明；
已知：如图，∠1＝∠4，∠2＝∠3，求证：AB∥CD；

证明：如图，延长CF交AB于点G

∵∠2＝∠3

∴BE∥CF（ ▲ ）

∴∠1＝ ▲ （两直线平行，同位角相等）

又∠1＝∠4

∴∠AGF＝ ▲ （ ▲ ）

∴AB∥CD（内错角相等，两直线平行）

查看试题解析
20. 疫情初期，武汉物资告急，全国一心，各地纷纷运送物资到武汉.已知3辆大货车与2辆小货车可以一次运货17吨，5辆大货车与4辆小货车可以一次运货29吨，则2辆大货车与1辆小货车可以一次运货多少吨？

查看试题解析
21. 如图，已知A（﹣1，2），B（3，2），C（4，4）.

(1)、请在网格中画出△ABC；

(2)、将△ABC向左平移3个单位长度，则在平移的过程中，线段AC扫过的图形面积为多少？

(3)、D为y轴上一点，且S_△ABD＝4，则D点坐标为.

查看试题解析
22. 某家具商先准备购进A，B两种家具，已知100件A型家具和150件B型家具需要35000元，150件A型家具和100件B型家具需要37500元.

(1)、求A，B两种家具每件各多少元；

(2)、家具商现准备了8500元全部用于购进这两种家具，他有几种方案可供选择？请你帮他设计出所有的购买方案.

查看试题解析
23. 如图1所示，AB∥CD，E为直线CD下方一点，BF平分∠ABE.

(1)、求证：∠ABE+∠C﹣∠E＝180°.

(2)、如图2，EG平分∠BEC，过点B作BH∥GE，求∠FBH与∠C之间的数量关系.

(3)、如图3，CN平分∠ECD，若BF的反向延长线和CN的反向延长线交于点M，且∠E+∠M＝130°，请直接写出∠E的度数.

查看试题解析
24. 平面直角坐标系中，A（a，0），B（0，b），a，b满足 ${(2 a + b + 5)}^{2} + \sqrt{a + 2 b - 2} = 0$ ，将线段AB平移得到CD，A，B的对应点分别为C，D，其中点C在y轴负半轴上.

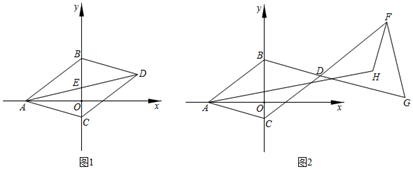(1)、求A，B两点的坐标；

(2)、如图1，连AD交BC于点E，若点E在y轴正半轴上，求 $\frac{B E - O E}{O C}$ 的值；

(3)、如图2，点F，G分别在CD，BD的延长线上，连结FG，∠BAC的角平分线与∠DFG的角平分线交于点H，求∠G与∠H之间的数量关系.

查看试题解析