湖北省武汉市硚口区2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-06-09 类型:期中考试
一、选择题
-
1. 下列各数中是无理数的是( )A、 B、 C、 D、2. 的平方根是( )A、 B、 C、 D、3. 在下列所给出坐标的点中,在第二象限的是( )A、(2,3) B、(﹣2,3) C、(﹣2,﹣3) D、(2,﹣3)4. 下列各式中,正确的是( )A、 B、 C、 D、5. 点M(2,﹣3)到x轴的距离是( )A、2 B、﹣3 C、3 D、以上都不对6. 如图,点 在 的延长线上,下列条件中不能判定 的是( )
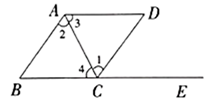 A、 B、 C、 D、7. 如图,学校相对于小明家的位置下列描述最准确的是( )
A、 B、 C、 D、7. 如图,学校相对于小明家的位置下列描述最准确的是( )
 A、距离学校 米处 B、北偏东 方向上的 米处 C、南偏西 方向上的 米处 D、南偏西 方向上的 米处8. 下列命题中,是真命题的是( )A、三条直线 、 、 在同一平面内,若a⊥b , b⊥c ,则 a⊥c B、无限小数都是无理数 C、经过直线外一点,有且只有一条直线与这条直线平行 D、同旁内角互补9. 如图,直线 ,点 在 上,点 、点 在 上, 的角平分线 交 于点 ,过点 作 于点 ,已知 ,则 的度数为( )
A、距离学校 米处 B、北偏东 方向上的 米处 C、南偏西 方向上的 米处 D、南偏西 方向上的 米处8. 下列命题中,是真命题的是( )A、三条直线 、 、 在同一平面内,若a⊥b , b⊥c ,则 a⊥c B、无限小数都是无理数 C、经过直线外一点,有且只有一条直线与这条直线平行 D、同旁内角互补9. 如图,直线 ,点 在 上,点 、点 在 上, 的角平分线 交 于点 ,过点 作 于点 ,已知 ,则 的度数为( )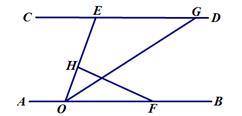 A、 B、 C、 D、10. 横、纵坐标均为整数的点称为整点.如图,一列有规律的整点,其坐标依次为 , , , , , , ,根据这个规律,第 个整点的坐标为( )
A、 B、 C、 D、10. 横、纵坐标均为整数的点称为整点.如图,一列有规律的整点,其坐标依次为 , , , , , , ,根据这个规律,第 个整点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 27的立方根为 .12. 点 在 轴上,则 .13. 点 关于 轴的对称点 的坐标是.14. 如图,已知 , ,第四象限的点 到 轴的距离为 ,若 , 满足 ,则 点坐标为; 与 轴的交点坐标为.
 15. 在同一平面内,若有 条直线,则最多有个交点;若 条直线中恰好有且只有 条直线互相平行,则这 条直线最多有个交点(用含有 的式子表示).16. 如图,在平面直角坐标系中,点 ,点 ,其中 , ,点 是 轴负半轴上一点,点 是在直线 与直线 之间的一点,连接 、 , 平分 , 平分 , 交 于 ,则 与 之间可满足的数量关系式为.
15. 在同一平面内,若有 条直线,则最多有个交点;若 条直线中恰好有且只有 条直线互相平行,则这 条直线最多有个交点(用含有 的式子表示).16. 如图,在平面直角坐标系中,点 ,点 ,其中 , ,点 是 轴负半轴上一点,点 是在直线 与直线 之间的一点,连接 、 , 平分 , 平分 , 交 于 ,则 与 之间可满足的数量关系式为.
三、解答题
-
17.(1)、计算:
①
② .
(2)、求下列式子中的 的值:① ,
② .
18. 如图,直线 , 相交于点 , ,垂足为 .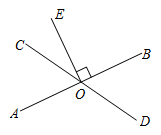 (1)、若 ,求 的度数;(2)、若 ,求 的度数.19. 完成下列证明:如图,已知 , , .
(1)、若 ,求 的度数;(2)、若 ,求 的度数.19. 完成下列证明:如图,已知 , , .求证: .

证明: , (已知)
, (▲)
(等量代换)
(▲)
(▲)
又 (已知)
▲ ▲(等量代换)
(▲)
(▲).
20. 如图,已知∠1=∠BDC,∠2+∠3=180°.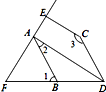 (1)、请你判断DA与CE的位置关系,并说明理由;(2)、若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.21. 如图,已知图中 点和 点的坐标分别为 和 .
(1)、请你判断DA与CE的位置关系,并说明理由;(2)、若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.21. 如图,已知图中 点和 点的坐标分别为 和 . (1)、请在图1中画出坐标轴建立适当的直角坐标系;(2)、写出点 的坐标为;(3)、连接 、 和 得 ,在 轴有点 满足 ,则点 的坐标为 , 个平方单位;(4)、已知第一象限内有两点 , 平移线段 使点 、 分别落在两条坐标轴上,则点 平移后的对应点的坐标是.22. 某小区有一块面积为 的正方形空地,开发商计划在此空地上沿边的方向建一个面积为 的长方形花坛,使长方形的长是宽的 倍.请你通过计算说明开发商能否实现这个愿望?23. 如图1, ,点 , 分别在 , 上, 射线 绕 点顺时针旋转至 便立即逆时针回转,射线 绕 点顺时针旋转至 便立即逆时针回转.射线 转动的速度是每秒 度,射线 转动的速度是每秒 度.
(1)、请在图1中画出坐标轴建立适当的直角坐标系;(2)、写出点 的坐标为;(3)、连接 、 和 得 ,在 轴有点 满足 ,则点 的坐标为 , 个平方单位;(4)、已知第一象限内有两点 , 平移线段 使点 、 分别落在两条坐标轴上,则点 平移后的对应点的坐标是.22. 某小区有一块面积为 的正方形空地,开发商计划在此空地上沿边的方向建一个面积为 的长方形花坛,使长方形的长是宽的 倍.请你通过计算说明开发商能否实现这个愿望?23. 如图1, ,点 , 分别在 , 上, 射线 绕 点顺时针旋转至 便立即逆时针回转,射线 绕 点顺时针旋转至 便立即逆时针回转.射线 转动的速度是每秒 度,射线 转动的速度是每秒 度. (1)、直接写出 的大小为;(2)、射线 、 转动后对应的射线分别为 、 ,射线 交直线 于点 ,若射线 比射线 先转动 秒,设射线 转动的时间为 秒,求 为多少时,直线 直线 ?(3)、如图2,若射线 、 同时转动 秒,转动的两条射线交于点 ,作 ,点 在 上,请探究 与 的数量关系.24. 如图1,在平面直角坐标系中,点 , ,点 在第三象限,已知 ,且 .
(1)、直接写出 的大小为;(2)、射线 、 转动后对应的射线分别为 、 ,射线 交直线 于点 ,若射线 比射线 先转动 秒,设射线 转动的时间为 秒,求 为多少时,直线 直线 ?(3)、如图2,若射线 、 同时转动 秒,转动的两条射线交于点 ,作 ,点 在 上,请探究 与 的数量关系.24. 如图1,在平面直角坐标系中,点 , ,点 在第三象限,已知 ,且 . (1)、求点 的坐标;(2)、如图2, 为线段 上一动点(端点除外), 是 轴负半轴的一点,连接 、 ,射线 与 的角平分线交于 ,若 ,求点 的坐标;
(1)、求点 的坐标;(2)、如图2, 为线段 上一动点(端点除外), 是 轴负半轴的一点,连接 、 ,射线 与 的角平分线交于 ,若 ,求点 的坐标;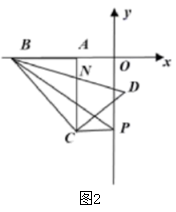 (3)、在第(2)问的基础上,如图3,点 与点 关于 轴对称, 是射线 上一个动点,连接 , 平分 , 平分 ,射线 .试问 的度数是否发生改变?若不变,请求其度数:若改变,请指出其变化范围.
(3)、在第(2)问的基础上,如图3,点 与点 关于 轴对称, 是射线 上一个动点,连接 , 平分 , 平分 ,射线 .试问 的度数是否发生改变?若不变,请求其度数:若改变,请指出其变化范围.