江苏省东台市第五联盟2020届九年级下学期数学期中考试试卷
试卷更新日期:2020-06-09 类型:期中考试
一、选择题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 下列几何体中,从正面看与从上面看不相同的是( )A、
 正方体
B、
正方体
B、 四棱锥
C、
四棱锥
C、 圆柱
D、
圆柱
D、 球
3. 下列运算正确的是( )A、a4•a2=a2 B、(a2)3=a5 C、(ab)2=a2b2 D、a2+a2=a44. 点P(1,﹣2)关于x轴对称的点的坐标为( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)5. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)6. 如图,AB∥DE,FG⊥BC于F,∠FGB=50°,则∠CDE=( )
球
3. 下列运算正确的是( )A、a4•a2=a2 B、(a2)3=a5 C、(ab)2=a2b2 D、a2+a2=a44. 点P(1,﹣2)关于x轴对称的点的坐标为( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)5. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)6. 如图,AB∥DE,FG⊥BC于F,∠FGB=50°,则∠CDE=( )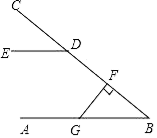 A、30° B、40° C、50° D、60°7. 如图,菱形ABCD的对角线AC、BD相交于点O.若周长为20,BD=8,则AC的长是( )
A、30° B、40° C、50° D、60°7. 如图,菱形ABCD的对角线AC、BD相交于点O.若周长为20,BD=8,则AC的长是( )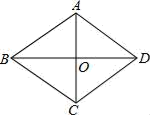 A、3 B、4 C、5 D、68. 如图,正比例函数y1=﹣2x的图象与反比例函数y2= 的图象交于A、B两点,点C在x轴负半轴上,AC=AO,△ACO的面积为6.则k的值为( )
A、3 B、4 C、5 D、68. 如图,正比例函数y1=﹣2x的图象与反比例函数y2= 的图象交于A、B两点,点C在x轴负半轴上,AC=AO,△ACO的面积为6.则k的值为( ) A、3 B、﹣3 C、﹣6 D、6
A、3 B、﹣3 C、﹣6 D、6二、填空题
-
9. 分解因式: .10. 计算:(2a+b)(2a﹣b)+b(2a+b)=.11. 若一元二次方程 有两个不相等的实数根,则k的取值范围是 .12. 二次函数 的最小值是 .
13. 如图,圆锥的底面半径为1 cm,母线AB的长为3 cm,则这个圆锥侧面展开图扇形的圆心角为度.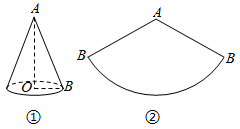 14. 如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A、D、E在同一条直线上,∠ACD=70°,则∠EDC的度数是.
14. 如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A、D、E在同一条直线上,∠ACD=70°,则∠EDC的度数是. 15. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为米(精确到0.1米).
15. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为米(精确到0.1米).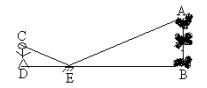 16. 如图,已知点 , , ,动点 在线段 上,点 、 、 按逆时针顺序排列,且 , ,当点 从点 运动到点 时,则点 运动的路径长为.
16. 如图,已知点 , , ,动点 在线段 上,点 、 、 按逆时针顺序排列,且 , ,当点 从点 运动到点 时,则点 运动的路径长为.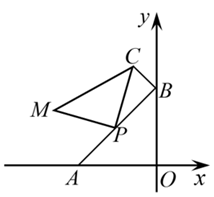
三、解答题
-
17.(1)、计算:(2)、解不等式组18. 先化简,再求值: ,其中x满足2x+6=019. 在▱ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
 (1)、求证:四边形BFDE是矩形;(2)、若CF=3,BF=4,DF=5,求证:AF平分∠DAB.20. 为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
(1)、求证:四边形BFDE是矩形;(2)、若CF=3,BF=4,DF=5,求证:AF平分∠DAB.20. 为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题: (1)、此次共调查了多少人?(2)、求体育社团在扇形统计图中所占圆心角的度数;(3)、请将条形统计图补充完整;(4)、若该校有3000名学生,请估计喜欢文学类社团的学生有多少人?21. 在一个不透明的口袋中装有1个红球,1个绿球和1个白球,这3个球除颜色不同外,其它都相同,从口袋中随机摸出1个球,记录其颜色,然后放回口袋搅匀,再从口袋中随机摸出1个球,记录其颜色,请利用画树状图或列表的方法,求两次摸到的球是一个红球和一个白球的概率.22. 为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次男子1000米耐力测试中,小明和小亮同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示:
(1)、此次共调查了多少人?(2)、求体育社团在扇形统计图中所占圆心角的度数;(3)、请将条形统计图补充完整;(4)、若该校有3000名学生,请估计喜欢文学类社团的学生有多少人?21. 在一个不透明的口袋中装有1个红球,1个绿球和1个白球,这3个球除颜色不同外,其它都相同,从口袋中随机摸出1个球,记录其颜色,然后放回口袋搅匀,再从口袋中随机摸出1个球,记录其颜色,请利用画树状图或列表的方法,求两次摸到的球是一个红球和一个白球的概率.22. 为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次男子1000米耐力测试中,小明和小亮同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示: (1)、当80≤t≤180时,求小明所跑的路程S(米)与所用的时间t(秒)之间的函数表达式;(2)、求他们第一次相遇的时间是起跑后的第几秒?23. 如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)、当80≤t≤180时,求小明所跑的路程S(米)与所用的时间t(秒)之间的函数表达式;(2)、求他们第一次相遇的时间是起跑后的第几秒?23. 如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(参考数据:sin69°≈ ,cos21°≈ ,tan20°≈ ,tan43°≈ ,所有结果精确到个位)
(1)、若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;(2)、若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?24. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC交AC于点E,AC的反向延长线交⊙O于点F. (1)、试判断直线DE与⊙O的位置关系,并说明理由;(2)、若∠C=30°,⊙O的半径为6,求弓形AF的面积.25. 华联超市准备代销一款运动鞋,每双的成本是170元,为了合理定价,投放市场进行试销.据市场调查,销售单价是200元时,每天的销售量是40双,而销售单价每降低1元,每天就可多售出5双,设每双降低x元(x为正整数),每天的销售利润为y元.(1)、求y与x的函数关系式;(2)、每双运动鞋的售价定为多少元时,每天可获得最大利润?最大利润是多少?26. 如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x.
(1)、试判断直线DE与⊙O的位置关系,并说明理由;(2)、若∠C=30°,⊙O的半径为6,求弓形AF的面积.25. 华联超市准备代销一款运动鞋,每双的成本是170元,为了合理定价,投放市场进行试销.据市场调查,销售单价是200元时,每天的销售量是40双,而销售单价每降低1元,每天就可多售出5双,设每双降低x元(x为正整数),每天的销售利润为y元.(1)、求y与x的函数关系式;(2)、每双运动鞋的售价定为多少元时,每天可获得最大利润?最大利润是多少?26. 如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x. (1)、求证:△PFA∽△ABE;(2)、若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;(3)、试求当x取何值时,以D为圆心,DP为半径的⊙D与线段AE只有一个公共点.27. 如图1,在平面直角坐标系中,直线 与 轴、 轴分别交于 、 两点,抛物线 经过 、 两点,与 轴的另一个交点为 .
(1)、求证:△PFA∽△ABE;(2)、若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;(3)、试求当x取何值时,以D为圆心,DP为半径的⊙D与线段AE只有一个公共点.27. 如图1,在平面直角坐标系中,直线 与 轴、 轴分别交于 、 两点,抛物线 经过 、 两点,与 轴的另一个交点为 .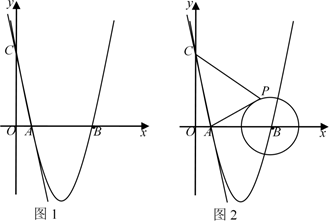 (1)、求抛物线的解析式及 点坐标;(2)、若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;(3)、如图2,若 点是半径为2的⊙ 上一动点,连接 、 ,当点 运动到某一位置时, 的值最小为.(直接写出结果)
(1)、求抛物线的解析式及 点坐标;(2)、若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;(3)、如图2,若 点是半径为2的⊙ 上一动点,连接 、 ,当点 运动到某一位置时, 的值最小为.(直接写出结果)