江苏省江阴市要塞片2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-06-09 类型：期中考试

进入出卷网下载

一、选择题

1. 下列图形中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若代数式 $\frac{2 x - 4}{x - 5}$ 有意义，则实数 x 的取值范围是（）

A、x = 5 B、x = 2 C、x≠5 D、x≠2

查看试题解析
3. 要反映台州市某一周每天的最高气温的变化趋势，宜采用( )

A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布统计图

查看试题解析
4. 分式：① $\frac{a + 2}{a^{2} + 3}$ ；② $\frac{a - b}{a^{2} - b^{2}}$ ；③ $\frac{4 a}{12 (a - b)}$ ；④ $\frac{1}{x - 2}$ 中，最简分式的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 在下列命题中，正确的是（）

A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的四边形是菱形 D、对角线互相垂直平分的四边形是菱形

查看试题解析
6.
如图，▱ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取值范围是（）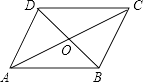

A、1＜m＜11 B、2＜m＜22 C、10＜m＜12 D、5＜m＜6

查看试题解析
7. 如果把分式 $\frac{3 n}{m^{2} - n^{2}}$ 中的m和n都扩大3倍，那么分式的值（）

A、不变 B、扩大3倍 C、缩小3倍 D、扩大9倍

查看试题解析
8. 若顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是（）

A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形

查看试题解析
9. 为改善城区居住环境,某市对4000米长的玉带河进行了绿化改造.为了尽快完成工期，施工队每天比原计划多绿化10米,结果提前2天完成.若原计划每天绿化 $x$ 米,则所列方程正确的是（）

A、 $\frac{4000}{x} - \frac{4000}{x + 10} = 2$ B、 $\frac{4000}{x + 10} - \frac{4000}{x} = 2$ C、 $\frac{4000}{x - 10} - \frac{4000}{x} = 2$ D、 $\frac{4000}{x} - \frac{4000}{x - 10} = 2$

查看试题解析
10. 如图，在四边形ABCD中，AB∥CD，∠C=90°，AB=8，AD=CD=5，点M为BC上异于B，C的一定点，点N为AB上的一动点，E，F分别为DM、MN的中点，当N从A到B的运动过程中，线段EF扫过图形的面积为（）

A、4 B、4.5 C、5 D、6

查看试题解析

二、填空题

11. 为了了解某区八年级6000名学生的体重情况，从中抽查了500名学生的体重，在这个问题中，样本为.

查看试题解析
12. 当 x =时，分式 $\frac{1 - x^{2}}{| x - 1 |}$ 的值是 0.

查看试题解析
13. 一个正三角形至少绕其中心旋转度，就能与其自身重合.

查看试题解析
14. 已知： $\frac{x}{3} = \frac{y}{4} = \frac{z}{5}$ ，则 $\frac{x + 2 y - 3 z}{x}$ =.

查看试题解析
15. 已知关于 x 的方程 $\frac{x - m}{x - 2}$ = 2的解是非负数，则 m 的取值范围是.

查看试题解析
16. 如图，在平行四边形ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是．

查看试题解析
17. 如图，矩形ABCD中， $A B = 15 cm$ ，点E在AD上，且 $A E = 9 cm$ ，连接EC，将矩形ABCD沿直线BE翻折，点A恰好落在EC上的点A'处，则 $A' C =$ cm.

查看试题解析
18. 如图，正方形ABCD 的边长为4，E 为AB 上一点，且AE=3 ，F 为BC 边上的一个动点，连接EF ，以EF 为边向左侧作等腰直角三角形FEG ，EG=EF，∠GEF=90°，连接AG ，则AG 的最小值为.

查看试题解析

三、解答题

19. 计算或化简

(1)、 $\frac{m^{2}}{m - 2} + \frac{4}{2 - m}$

(2)、 $\frac{x^{2} - 4}{x^{2} + 2 x + 1} \div (x + 2) \cdot \frac{x + 1}{2 - x}$

查看试题解析
20. 解分式方程：

(1)、 $\frac{5}{2 x - 1} = \frac{3}{x + 2}$

(2)、 $\frac{x - 2}{x + 2} - \frac{16}{x^{2} - 4} = 1$

查看试题解析
21. 先化简，再求值： $(\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4}) \div \frac{x - 4}{x}$ ，其中x²﹣4x﹣1=0.

查看试题解析
22. 如图，四边形ABCD是平行四边形，E、F是对角线AC上的两点，∠1=∠2．

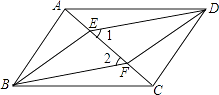(1)、求证：AE=CF；

(2)、求证：四边形EBFD是平行四边形．

查看试题解析
23. 如图，点O是菱形ABCD对角线的交点， $C E / / B D ， E B / / A C$ ，连接OE，交BC于F.

(1)、求证： $O E = C B$ ；

(2)、如果OC： $O B = 1$ ： $2 ， O E = \sqrt{5}$ ，求菱形ABCD的面积.

查看试题解析
24. “低碳环保，你我同行”.两年来，扬州市区的公共自行车给市民出行带来切实方便.电视台记者在某区街头随机选取了市民进行调查，调查的问题是“您大概多久使用一次公共自行车”，将本次调查结果归为四种情况：A.每天都用；B.经常使用；C.偶尔使用；D.从未使用.将这次调查情况整理并绘制如下两幅统计图如图2：

根据图中的信息，解答下列问题：

(1)、本次活动共有位市民参与调查；

(2)、补全条形统计图和扇形统计图；

(3)、扇形统计图中A项所对应的圆心角的度数为；

(4)、根据统计结果，若该区有46万市民，请估算每天都用公共自行车的市民约有多少人.

查看试题解析
25. 六一期间，某公园游戏场举行“迎奥运”活动．有一种游戏的规则是：在一个装有6个红球和若干个白球（每个球除颜色外其他相同）的袋中，随机摸一个球，摸到一个红球就得到一个奥运福娃玩具．已知参加这种游戏活动为40000人次，公园游戏场发放的福娃玩具为10000个．

(1)、求参加一次这种游戏活动得到福娃玩具的概率

(2)、请你估计袋中白球接近多少个？

查看试题解析
26. 2018年我市的脐橙喜获丰收，脐橙一上市，水果店的陈老板用2400元购进一批脐橙，很快售完；陈老板又用6000元购进第二批脐橙，所购件数是第一批的2倍，但进价比第一批每件多了20元.

(1)、第一批脐橙每件进价多少元？

(2)、陈老板以每件120元的价格销售第二批脐橙，售出 $60 %$ 后，为了尽快售完，决定打折促销，要使第二批脐橙的销售总利润不少于480元，剩余的脐橙每件售价最低打几折？(利润＝售价－进价)

查看试题解析
27.
如图，P为正方形ABCD的边BC上一动点（P与B、C不重合），连接AP，过点B作BQ⊥AP交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交BA的延长线于点M．

(1)、试探究AP与BQ的数量关系，并证明你的结论

(2)、当AB=3，BP=2PC，求QM的长；

(3)、当BP=m，PC=n时，求AM的长.

查看试题解析
28.
已知：如图①，在矩形ABCD中，AB=5，AD= $\frac{20}{3}$ ，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF，BF．

(1)、求AE和BE的长；

(2)、若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点F分别平移到线段AB、AD上时，直接写出相应的m的值；

(3)、如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P．与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．

查看试题解析