江苏省东台市第五联盟2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-06-09 类型：期中考试

进入出卷网下载

一、选择题

1. 下列电视台的台标，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中,随机事件是（）

A、三角形中任意两边之和大于第三边 B、太阳从东方升起 C、明天会下雨 D、一个有理数的绝对值为负数

查看试题解析
3. “学习强国”的英语“Learningpower”中，字母“n”出现的频率是（）

A、 $\frac{2}{13}$ B、 $\frac{1}{12}$ C、2 D、1

查看试题解析
4. 分式 $- \frac{1}{1 - x}$ 可变形为（）

A、 $- \frac{1}{x - 1}$ B、 $\frac{1}{x - 1}$ C、 $- \frac{1}{1 + x}$ D、 $\frac{1}{1 + x}$

查看试题解析
5. 在常见的统计图中，能清楚地反映每个部分在总体中所占百分比的统计图是（）

A、扇形统计图 B、条形统计图 C、折线统计图 D、频率分布直方图

查看试题解析
6. 若把分式 $\frac{2 x y}{x - y}$ 中的 $x$ 和 $y$ 都扩大为原来的5倍，那么分式的值（）

A、扩大为原来的5倍 B、扩大为原来的10倍 C、不变 D、缩小为原来的 $\frac{1}{5}$ 倍

查看试题解析
7. 如图所示，在▱ABCD中，AD＝5，AB＝3，AE平分∠BAD交BC边于点E，则线段BE、CE的长分别是（）

A、2和3 B、3和2 C、4和1 D、1和4

查看试题解析
8. 如图，在平面直角坐标系中， $▱ A B C D$ 的顶点坐标分别为 $A (3 ， a)$ ， $B (2 ， 2)$ ， $C (b ， 3)$ ， $D (8 ， 6)$ ，则a+b的值为（）

A、8 B、9 C、12 D、11

查看试题解析

二、填空题

9. 为了了解我市60000名学生参加初中毕业升学数学考试的成绩情况，从中抽取了200名考生的成绩进行统计，在这个问题中，样本容量是.

查看试题解析
10. 当x=时，分式 $\frac{x - 2}{x + 2}$ 的值为零．

查看试题解析
11.
小明把如图所示的矩形纸板挂在墙上，玩飞镖游戏（每次飞镖均落在纸板上），则飞镖落在阴影区域的概率是．

查看试题解析
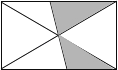12. 如图，转盘中8个扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，估计下列事件发生的可能性的大小，并将这些事件的序号按发生的可能性从小到大的顺序排成一列是.（填序号）

（ 1 ）指针落在标有3的区域内；（ 2 ）指针落在标有9的区域内；

（ 3 ）指针落在标有数字的区域内；（ 4 ）指针落在标有奇数的区域内.

查看试题解析
13. 如图，已知矩形ABCD，P、R分别是BC和DC上的动点，E、F分别是PA、PR的中点.如果DR＝5，AD＝12，则EF的长为.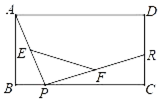

查看试题解析
14. 若分式 $\frac{6}{m - 2}$ 的值是正整数，则m可取的整数有．

查看试题解析
15. 如图，四边形ABCD是菱形，对角线AC＝8cm，DB＝6cm，DH⊥AB于点H，则DH的长为.

查看试题解析
16. 如图，将锐角为 $45^{\circ}$ 的直角三角板MPN的一个锐角顶点P与边长为4的正方形ABCD的顶点A重合，正方形ABCD固定不动，然后将三角板绕着点A旋转， $∠ MPN$ 的两边分别与正方形的边BC、DC或其延长线相交于点E、F，连结EF.在三角板旋转过程中，当 $∠ MPN$ 的一边恰好经过BC边的中点时，则EF的长为.

查看试题解析

三、解答题

17. 解方程：

(1)、 $\frac{2}{x - 2} = \frac{3}{x + 3}$

(2)、 $\frac{3}{4 - x} + 2 = \frac{1 - x}{x - 4}$

查看试题解析
18. 先化简 $(1 - \frac{3}{a + 2}) \div \frac{a^{2} - 2 a + 1}{a^{2} - 4}$ ，再从-2、2、0 、1四个数中选一个恰当的数作为a的值代入求值.

查看试题解析
19. 某校八年级学生全部参加“初二生物地理会考”，从中抽取了部分学生的生物考试成绩，将他们的成绩进行统计后分为A，B，C，D四等，并将统计结果绘制成如下的统计图，请结合图中所给的信息解答下列问题

(1)、抽取了名学生成绩；

(2)、请把条形统计图补充完整；

(3)、扇形统计图中等级D所在的扇形的圆心角度数是；

(4)、若A，B，C代表合格，该校初二年级有300名学生，求全年级生物合格的学生共约多少人

查看试题解析
20. 如图，在▱ABCD中，已知点E、F分别在边BC和AD上，且BE=DF.求证：AE=CF.

查看试题解析
21. 正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：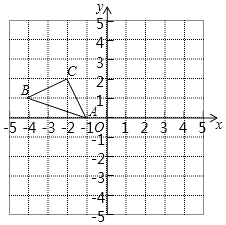

(1)、作出△ABC绕点A逆时针旋转90°的△A₁B₁C₁；作出△ABC关于原点O成中心对称的△A₂B₂C₂；

(2)、点B₁的坐标为，点C₂的坐标为

查看试题解析
22. 书店老板去图书批发市场购买某种图书，第一次用1200元购买若干本，很快售完.第二次购买时，每本书的进价比第一次提高了20%，他用1500元所购买的数量比第一次多10本.求第一次购买的图书，每本进价多少元？

查看试题解析
23. 如图，四边形ABCD为矩形，点E是边BC的中点，AF∥ED，AE∥DF

(1)、求证：四边形AEDF为菱形；

(2)、试探究：当AB：BC＝▲ ，菱形AEDF为正方形？请说明理由.

查看试题解析
24. 操作体验：如图，在矩形ABCD中，点E、F分别在边AD、BC上，将矩形ABCD沿直线EF折叠，使点D恰好与点B重合，点C落在点C'处.点P为直线EF上一动点(不与E、F重合)，过点P分别作直线BE、BF的垂线，垂足分别为点M和N，以PM、PN为邻边构造平行四边形PMQN.

(1)、如图1，求证：BE=BF；

(2)、特例感知：如图2，若DE=5，CF=3，当点P在线段EF上运动时，求平行四边形PMQN的周长；

(3)、类比探究：如图3，当点P在线段EF的延长线上运动时，若DE=a，CF=b.请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)

查看试题解析