河南省洛阳市偃师市2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-06-09 类型:期中考试
一、选择题
-
1. 在式子中,分式的个数有( )A、2 B、3 C、4 D、52. 若分式 的值为0,则 的值是( )A、2 B、0 C、-2 D、-53. 将 , , 这三个数按从小到大的顺序排列,正确的结果是( )A、 < < B、 < < C、 < < D、 < <4. 生物学家发现一种病毒的长度约为0.000043mm,用科学记数法表示这个数的结果为(单位:mm)( )A、4.3×10﹣5 B、4.3×10﹣4 C、4.3×10﹣6 D、43×10﹣55. 函数 的自变量x的取值范围是( )A、 B、 C、 D、6. 某反比例函数的图象经过点(-2,3),则此函数图象也经过( )A、(2,-3) B、(-3,3) C、(2,3) D、(-4,6)7. 一次函数y=ax+b与反比例函数 的图象如图所示,则( )
 A、a>0,b>0,c>0 B、a<0,b<0,c<0 C、a<0,b>0,c>0 D、a<0,b<0,c>08. 已知如图,一次函数y=ax+b和反比例函数y= 的图象相交于A、B两点,不等式ax+b> 的解集为( )
A、a>0,b>0,c>0 B、a<0,b<0,c<0 C、a<0,b>0,c>0 D、a<0,b<0,c>08. 已知如图,一次函数y=ax+b和反比例函数y= 的图象相交于A、B两点,不等式ax+b> 的解集为( )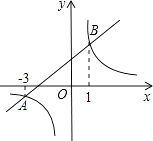 A、x<﹣3 B、﹣3<x<0或x>1 C、x<﹣3或x>1 D、﹣3<x<19. 反比例函数 图象上三个点的坐标为 、 、 ,若 ,则 的大小关系是( )A、 B、 C、 D、10. 下列图像中, 不是 的函数的是( )A、
A、x<﹣3 B、﹣3<x<0或x>1 C、x<﹣3或x>1 D、﹣3<x<19. 反比例函数 图象上三个点的坐标为 、 、 ,若 ,则 的大小关系是( )A、 B、 C、 D、10. 下列图像中, 不是 的函数的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 当x时,分式 有意义.12. 当m=时,方程 会产生增根。13. 反比例函数 y =(a-3)x| a | - 4 的函数值为4时,自变量 x 的值是.14. 已知点P(a,b)在一次函数y=4x+3的图象上,则代数式4a﹣b﹣2的值等于 .15. 如图,已知反比例函数y=
 (k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B,若△AOB的面积为1,则k=.
(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B,若△AOB的面积为1,则k=. 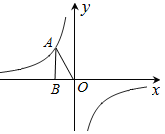
三、解答题
-
16. 先化简,再求值: ,其中 .17. 先化简.再求值
已知 ,求 的值.
18. 解方程19. 在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍,求降价后每枝玫瑰的售价是多少元?20. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(-3,m+8),B(n,-6)两点.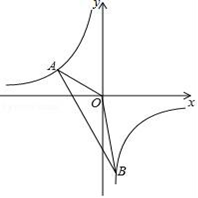 (1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积.21. 已知反比例函数y= 的图象的一支位于第一象限.
(1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积.21. 已知反比例函数y= 的图象的一支位于第一象限. (1)、判断该函数图象的另一支所在的象限,并求m的取值范围;
(1)、判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)、如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.22. 某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费 (元)是行李质量 ( )的一次函数.已知行李质量为 时需付行李费 元,行李质量为 时需付行李费 元.
(1)、当行李的质量 超过规定时,求 与 之间的函数表达式;(2)、求旅客最多可免费携带行李的质量.23. 如图,已知A(-4, )、B(2,-4)是一次函数 的图象和反比例函数 的图象的两个交点. (1)、求反比例函数和一次函数的解析式;(2)、求直线AB和 轴的交点C的坐标;(3)、求方程 的解(请直接写出答案);(4)、求不等式 的解集(请直接写出答案).
(1)、求反比例函数和一次函数的解析式;(2)、求直线AB和 轴的交点C的坐标;(3)、求方程 的解(请直接写出答案);(4)、求不等式 的解集(请直接写出答案).