辽宁省锦州市北镇市2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-06-08 类型：期中考试

进入出卷网下载

一、选择题

1. “x的2倍与3的差不大于8”列出的不等式是（）

A、 $2 x - 3 \leq 8$ B、 $2 x - 3 \geq 8$ C、 $2 x - 3 < 8$ D、 $2 x - 3 > 8$

查看试题解析
2. 若等腰三角形的两条边长分别为2和4，则该等腰三角形的周长为（）

A、6 B、8 C、10 D、8或10

查看试题解析
3. 如图，将△ABC沿直线AB向右平移后到达△BDE的位置，若∠CAB=50º，∠ABC=100º，则∠CBE的度数为（）

A、45° B、30° C、20° D、15°

查看试题解析
4. 如图，若一次函数y＝﹣2x+b的图象与两坐标轴分别交于A，B两点，点A的坐标为（0，3），则不等式﹣2x+b＞0的解集为（）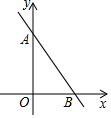

A、x＞ $\frac{3}{2}$ B、x＜ $\frac{3}{2}$ C、x＞3 D、x＜3

查看试题解析
5. 如图，在Rt△ABC中，∠ACB=90º，∠A=60º，CD是斜边AB上的高，若AD=3cm，则斜边AB的长为（）

A、3cm B、6cm C、9cm D、12cm

查看试题解析
6. 如图，AD是 $△ A B C$ 的角平分线，且 $A B ： A C$ = $\sqrt{3} ： \sqrt{2}$ ，则 $△ A B D$ 与 $△ A C D$ 的面积之比为（）

A、 $\sqrt{2} ： \sqrt{3}$ B、 $2 ： 3$ C、 $\sqrt{3} ： \sqrt{2}$ D、 $3 ： 2$

查看试题解析
7. 如图，在△ABC中，BD平分∠ABC，BC的垂直平分线交BD于点E，连接CE，若∠A=60°，∠ACE=24°，则∠ABE的度数为（）

A、24° B、30° C、32° D、48°

查看试题解析
8. 如图，等边△OAB的顶点O为坐标原点，AB∥x轴，OA=2，将等边△OAB绕原点O顺时针旋转105º至△OCD的位置，则点D的坐标为（）

A、(2，-2) B、( $\sqrt{3}$ ， $- \sqrt{3}$ ) C、( $\sqrt{2}$ ， $\sqrt{2}$ ) D、( $\sqrt{2}$ ， $- \sqrt{2}$ )

查看试题解析

二、填空题

9. 要用反证法证明命题“一个三角形中不可能有两个角是直角”，首先应假设这个三角形中．

查看试题解析
10. 根据不等式的基本性质，可将“mx＜2”化为“x＞ $\frac{2}{m}$ ”，则m的取值范围是.

查看试题解析
11. 如图，点D为等边△ABC内部一点，且∠ABD=∠BCD，则∠BDC的度数为.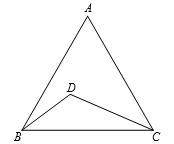

查看试题解析
12. 如图，在Rt△ABC中，∠B=90°，AB=9，BC=6，将△ABC折叠，使点A与BC的中点D重合，折痕为EF，则BE的长为.

查看试题解析
13. 在△ABC，AB＝AC＝5，BC＝6，若点P在边AC上移动，则BP的最小值是.

查看试题解析
14. 若不等式组 ${\begin{matrix} 2 x - b \geq 0 \\ x + a \leq 0 \end{matrix}$ 的解集为3≤x≤4，则不等式ax+b＜0的解集为．

查看试题解析
15. 如图，在△ABC中，∠C=90°，AC=BC，AD平分∠BAC交BC于点D，DE⊥AB于点E，若△BDE的周长为6，则AC=.

查看试题解析
16. 如图，∠MON=30°，点A₁ ， A₂ ， A₃ ， …在射线ON上，点B₁ ， B₂ ， B₃ ， …在射线OM上，△A₁B₁A₂ ， △A₂B₂A₃ ， △A₃B₃A₄…均为等边三角形.若OA₁=1，则△A_nB_nA_n+1的边长为.

查看试题解析

三、解答题

17. 解不等式（组）：

(1)、解不等式 $\frac{x - 5}{2} + 1 > x - 3$ ，并把它的解集表示在数轴上；

(2)、解不等式组： ${\begin{array}{l} 2 x + 5 \geq 3 (x + 2) ， \\ \frac{1 - 2 x}{3} + \frac{1}{5} > 0. \end{array}$

查看试题解析
18. 如图，已知一次函数y₁=-x+b的图象交x轴于点A（3，0），与一次函数y₂= $\frac{1}{2}$ x+1的图象交于点B.

(1)、求一次函数y₁=-x+b的表达式；

(2)、当x取哪些值时，0<y₁<y₂？

查看试题解析
19. 如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为(2，4).

(1)、AB的长等于；

(2)、画出△ABC向下平移5个单位后得到△A₁B₁C₁ ，并写出此时点A₁的坐标；

(3)、画出△ABC绕原点O旋转180º后得到的△A₂B₂C₂ ，并写出此时点C₂的坐标.

查看试题解析
20. 如图，在Rt△ABC中，∠ACB＝90°，D是AB上一点，BD＝BC，过点D作AB的垂线交AC于点E，连接CD，交BE于点F.
求证：BE垂直平分CD.

查看试题解析
21. A，B两种型号的空调，已知购进3台A型号空调和5台B型号空调共用14500元；购进4台A型号空调和10台B型号空调共用25000元.

(1)、求A，B两种型号空调的进价；

(2)、若超市准备用不超过54000元的资金再购进这两种型号的空调共30台，求最多能购进A种型号的空调多少台？

查看试题解析
22. 如图，在等边△ABC中，点D，E分别在边AC，AB上，且AD=BE，BD，CE交于点P，CF⊥BD，垂足为点F.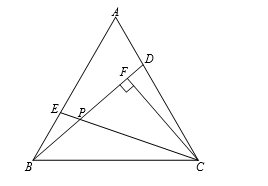

(1)、求证：BD=CE；

(2)、若PF=3，求CP的长.

查看试题解析
23. 现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品x千克．

(1)、请分别写出甲、乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；

(2)、小明选择哪家快递公司更省钱？

查看试题解析
24. 已知OP平分∠AOB，∠DCE的顶点C在射线OP上，射线CD交射线OA于点F，射线CE交射线OB于点G.

(1)、如图1，若CD⊥OA，CE⊥OB，请直接写出线段CF与CG的数量关系；

(2)、如图2，若∠AOB=120º，∠DCE=∠AOC，试判断线段CF与CG的数量关系，并说明理由.

查看试题解析