辽宁省鞍山市铁东区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-06-08 类型:期中考试
一、选择题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列二次根式,化简后能与 合并的是( )A、 B、 C、 D、3. 如图,在四边形 中, ,要使四边形 是平行四边形,下列可添加的条件不正确的是( )
 A、 B、 C、 D、4. 以下列各组数为边长,能构成直角三角形的是( )A、 B、 C、 D、5. 已知 是整数,则满足条件的最小正整数n为( )A、1 B、2 C、3 D、126. 如图, ,则数轴上点C所表示的数为( ).
A、 B、 C、 D、4. 以下列各组数为边长,能构成直角三角形的是( )A、 B、 C、 D、5. 已知 是整数,则满足条件的最小正整数n为( )A、1 B、2 C、3 D、126. 如图, ,则数轴上点C所表示的数为( ). A、 B、 C、 D、7. 如图,从一个大正方形中裁去面积为 和 的两个小正方形,则余下部分的面积为( )
A、 B、 C、 D、7. 如图,从一个大正方形中裁去面积为 和 的两个小正方形,则余下部分的面积为( )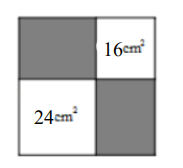 A、 B、 C、 D、8. 如图,在 中, 平分 ,则 ( )
A、 B、 C、 D、8. 如图,在 中, 平分 ,则 ( )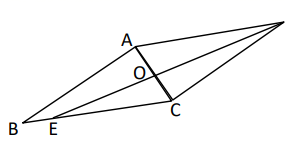 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
9. 命题“两直线平行,同位角相等”的逆命题是。10. 若 在实数范围内有意义,则x的取值范围.11. 如图,在 中,若 , 则 的大小为.
 12. 计算 的结果是.13. 已知: ,则 .14. 已知,如图,一小船以20海里/时的速度从港口A出发向东北方向航行,另一小船以15海里/时的速度同时从港口A出发向东南方向航行,离开港口1小时后,则两船相距.
12. 计算 的结果是.13. 已知: ,则 .14. 已知,如图,一小船以20海里/时的速度从港口A出发向东北方向航行,另一小船以15海里/时的速度同时从港口A出发向东南方向航行,离开港口1小时后,则两船相距. 15. 如图,四边形ABCD是平行四边形, ,顶点A在y轴上,边BC在x轴上,且点B的坐标为(-4,0),设点P是边BC上(不与点B、C重合)的一个动点,则当 为等腰三角形时点P的坐标是.
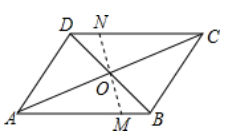
15. 如图,四边形ABCD是平行四边形, ,顶点A在y轴上,边BC在x轴上,且点B的坐标为(-4,0),设点P是边BC上(不与点B、C重合)的一个动点,则当 为等腰三角形时点P的坐标是. 16. 如图,平行四边形纸片 中, ,将平行四边形纸片 折叠,使点A与点C重合,则下列结论正确的是.
16. 如图,平行四边形纸片 中, ,将平行四边形纸片 折叠,使点A与点C重合,则下列结论正确的是.① ;② ;③ ;④
三、解答题
-
17. 计算:(1)、(2)、18. 如图,平行四边形ABCD的对角线AC、BD,相交于点O,EF过点O且与AB、CD分别相交于点E、F,求证:AE=CF.
 19. 观察下列等式:
19. 观察下列等式:① ,
②
③
······
回答下列问题:
(1)、仿照上列等式,写出第n个等式:;(n是正整数)(2)、按上述方法,化简: .( 要求写过程)20. 如图,以 为边作 和 ,连接 .求证:四边形 是平行四边形.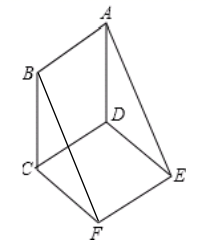 21. 如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,若C在格点上,且满足 .
21. 如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,若C在格点上,且满足 . (1)、在图中画出符合条件的 ;(2)、若 于点D,则BD的长为.22. 如图,在四边形 中, 交于点 分别为垂足, .
(1)、在图中画出符合条件的 ;(2)、若 于点D,则BD的长为.22. 如图,在四边形 中, 交于点 分别为垂足, .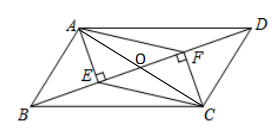 (1)、求证:试判断四边形 形状,并说明理由;(2)、如果 ,求BC.
(1)、求证:试判断四边形 形状,并说明理由;(2)、如果 ,求BC.

