江苏省宜兴市和桥联盟2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-06-08 类型：期中考试

进入出卷网下载

一、选择题

1. 以下问题，不适合用普查的是（）

A、了解全班同学每周体育锻炼的时间 B、了解一批灯泡的使用寿命 C、学校招聘教师，对应聘人员面试 D、了解“神舟二号”飞船零部件的状况

查看试题解析
2. 为了解无锡市 2018 年中考数学学科各分数段成绩分布情况，从中抽取 150 名考生的数学成绩进行统计分析.在这个问题中，样本是指（）

A、150 B、无锡市 2017 年中考数学成绩 C、被抽取的 150 名考生 D、被抽取的 150 名考生的中考数学成绩

查看试题解析
3. 下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列分式中是最简分式的是（）

A、 $\frac{2 x}{x^{2} + 1}$ B、 $\frac{4}{2 x}$ C、 $\frac{x - 1}{x^{2} - 1}$ D、 $\frac{1 - x}{x - 1}$

查看试题解析
5. 下列性质中，平行四边形一定具有的性质是（）

A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边互相垂直

查看试题解析
6. 若分式 $\frac{x - 3}{x + 3}$ 的值为0，则x的值为（）

A、3 B、-3 C、3或-3 D、0

查看试题解析
7. 分式 $\frac{a + b}{a b}$ (a、b均为正数)，字母的值都扩大为原来的2倍，则分式的值（）

A、扩大为原来的2倍 B、缩小为原来的 $\frac{1}{2}$ C、不变 D、缩小为原来的 $\frac{1}{4}$

查看试题解析
8. 今年我市工业试验区投资50760万元开发了多个项目，今后还将投资106960万元开发多个新项目，每个新项目平均投资比今年每个项目平均投资多500万元，并且新增项目数量比今年多20个.假设今年每个项目平均投资是x万元，那么下列方程符合题意的是（）

A、 $\frac{106960}{x + 500} - \frac{50760}{x} = 20$ B、 $\frac{50760}{x} - \frac{106960}{x + 500} = 20$ C、 $\frac{106960}{x + 20} - \frac{50760}{x} = 500$ D、 $\frac{50760}{x} - \frac{106960}{x + 20} = 500$

查看试题解析
9. 矩形ABCD与CEFG，如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH．若BC=EF=2，CD=CE=1，则GH=（）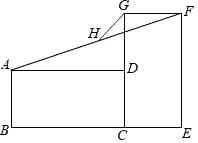

A、1 B、 $\frac{2}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析
10. 如图，在边长为4的正方形ABCD中，点E、F分别是边BC、CD上的动点，且BE＝CF，连接BF、DE，则BF＋DE的最小值为（）

A、 $\sqrt{12}$ B、 $\sqrt{20}$ C、 $\sqrt{48}$ D、 $\sqrt{80}$

查看试题解析

二、填空题

11. 要使分式 $\frac{5}{x - 3}$ 有意义，则x的取值范围是.

查看试题解析
12. 一个不透明的口袋中有质地均匀大小相同的1个白球和2个黑球，从中任意摸出1个球，摸出白球的概率是.

查看试题解析
13. 如图，在▱ABCD中，对角线AC、BD相交于点O，在不添加任何辅助线的情况下，请你添加一个条件，使▱ABCD是菱形.

查看试题解析
14. 若x-y≠0，x-2y=0，则分式 $\frac{10 x - 11 y}{x - y}$ 的值．

查看试题解析
15. 一个样本的50个数据分别落在5个小组内，第1、2、3、4组的数据的个数分别为2、8、15、5，则第5组的频率为。

查看试题解析
16. 已知菱形ABCD的对角线AC=10，BD=24，则此菱形的周长为.

查看试题解析
17. 如图，矩形ABCD的对角线AC与BD相交点O，AC=12，P，Q分别为AO，AD的中点，则PQ的长度为.

查看试题解析
18. 如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90⁰ ，连结AC，若AC=10，则四边形ABCD的面积为.

查看试题解析

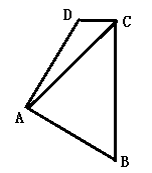
三、解答题

19. 化简：

(1)、 $\frac{2}{x} - \frac{5}{x^{2}}$

(2)、 $(1 + \frac{1}{a - 1}) (\frac{1}{a^{2}} - 1)$

查看试题解析
20. 解方程：

(1)、 $\frac{1}{x} = \frac{5}{x + 3}$

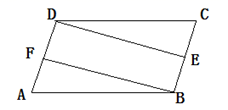
(2)、 $\frac{3 - x}{x - 4} - \frac{1}{4 - x} = 1$

查看试题解析
21. 先化简代数式再求值 $(\frac{a + 2}{a - 2} + \frac{4}{a^{2} - 4 a + 4}) \div \frac{a}{a - 2}$ ，其中 $a = 3$ .

查看试题解析
22. 如图，在▱ABCD中，E、F分别是边BC、AD的中点，求证：∠ADE=∠CBF

查看试题解析
23. 某校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学这餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图.

(1)、这次被调查的同学共有人；

(2)、补全条形统计图，并在图上标明相应的数据；

(3)、校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算，该校18000名学生一餐浪费的食物可供多少人食用一餐.

查看试题解析
24. 小明用12元买软面笔记本，小丽用21元买硬面笔记本.

(1)、已知每本硬面笔记本比软面笔记本贵1.2元，小明和小丽能买到相同数量的笔记本吗；

(2)、已知每本硬面笔记本比软面笔记本贵a元，是否存在正整数a，使得每本硬面笔记本、软面笔记本的价格都是正整数，并且小明和小丽能买到相同数量的笔记本？若存在，求出a的值；若不存在，请说明理由.

查看试题解析
25. 如图，在10×10的网格中，有一格点三角形ABC.（说明：顶点都在网格线交点处的三角形叫做格点三角形）

(1)、将△ABC绕点C旋转180°，得到△A′B′C，请直接画出旋转后的△A′B′C.（友情提醒：别忘了标上相应的字母!）

(2)、在网格中以AB为一边作格点△ABD（顶点在小正方形的顶点处的三角形称为格点三角形），使它的面积是△ABC的2倍，则点D的个数有个.

查看试题解析
26. 如图，平行四边形ABCD中，AB⊥AC，AB=2，AC=4.对角线AC、BD相交于点O，将直线AC绕点O顺时针旋转 $α$ °（0°＜ $α$ ＜180°），分别交直线BC、AD于点E、F.

(1)、当 $α$ =°时，四边形ABEF是平行四边形；

(2)、在旋转的过程中，从A、B、C、D、E、F中任意4个点为顶点构造四边形，
①当 $α$ =_▲_°时，构造的四边形是菱形；

②若构造的四边形是矩形，求该矩形的两边长.

查看试题解析