江苏省无锡市滨湖区2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-06-08 类型：期中考试

进入出卷网下载

一、选择题

1. 下列图形中，是轴对称但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 要使分式 $\frac{1}{a + 3}$ 有意义，则a的取值应满足（）

A、 $a = - 3$ B、 $a \neq - 3$ C、 $a > - 3$ D、 $a \neq 3$

查看试题解析
3. 分式 $- \frac{1}{2 - x}$ 可变形为（）

A、 $- \frac{1}{x - 2}$ B、 $\frac{1}{x + 2}$ C、 $- \frac{1}{x + 2}$ D、 $\frac{1}{x - 2}$

查看试题解析
4. 下列说法正确的是（）

A、为了了解某中学1200名学生的视力情况，从中随机抽取了50名学生进行调查，在此次调查中，样本容量为50名学生的视力 B、若一个游戏的中奖率是2%，则做50次这样的游戏一定会中奖 C、了解无锡市每天的流动人口数，采用抽样调查方式 D、“掷一枚硬币，正面朝上”是必然事件

查看试题解析
5. 掷一枚普通的正六面体骰子，出现的点数中，以下结果机会最大的是（）

A、点数为3的倍数 B、点数为奇数 C、点数不小于4 D、点数不大于4

查看试题解析
6. 下列约分正确的是（）

A、 $\frac{x^{6}}{x^{2}} = x^{3}$ B、 $\frac{x + y}{x + y} = 0$ C、 $\frac{2 x y^{2}}{4 x^{2} y} = \frac{1}{2}$ D、 $\frac{a + b}{x (a + b)} = \frac{1}{x}$

查看试题解析
7. 矩形具有而平行四边形不一定具有的性质是（）

A、对边平行且相等 B、对角相等 C、对角线互相平分 D、对角线相等

查看试题解析
8. 计算 $(x y - x^{2}) \div \frac{x - y}{x y}$ 的结果为（）

A、 $\frac{1}{y}$ B、 $x^{2} y$ C、 $- x^{2} y$ D、 $- x y$

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ A = 70 ° ， A C = B C$ ，以点B为旋转中心把 $△ A B C$ 按顺时针旋转一定角度，得到 $△ A' B C^{'} ，$ 点 $A'$ 恰好落在 $A C$ 上，连接 $C C^{'} ，$ 则 $∠ A C C^{'}$ 度数为（）

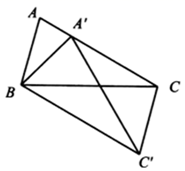A、110° B、100° C、90° D、70°

查看试题解析
10. 如图，在菱形 $A B C D$ 中， $∠ D = 135 °$ ， $A D = 3 \sqrt{2} ， C E = 2$ ，点P是线段AC上一动点，点F是线段AB上一动点，则 $P E + P F$ 的最小值（）

A、 $2 \sqrt{2}$ B、3 C、 $2 \sqrt{5}$ D、 $\sqrt{10}$

查看试题解析

二、填空题

11. 在代数式 $\frac{x + 1}{5}, \frac{1}{x}, \frac{x}{2}$ 中，分式有个.

查看试题解析
12. 分式 $\frac{1}{2 x^{2} y}, \frac{1}{6 x y^{3}}$ 的最简公分母是.

查看试题解析
13. 当x=时，分式 $\frac{x^{2} - 4}{x - 2}$ 的值等于零．

查看试题解析
14. 在一个不透明的口袋中装有若干个质地相同，而颜色不完全相同的球，如果口袋中只装有4个黄球，且摸出黄球的概率为 $\frac{1}{3}$ ，那么袋中共有个球.

查看试题解析
15. 四张质地、大小、背面完全相同的卡片上，正面分别画有平行四边形、矩形、等腰三角形、菱形四个图案.现把它们的正面向下随机摆放在桌面上，从中任意抽出一张，则抽出的卡片正面图案是中心对称图形的概率为.

查看试题解析
16. 矩形 $A B C D$ 中， $A B = 5 ， B C = 4 ， E 、 F$ 分别在AB、CD上，且EF垂直平分AC.则AE的长为.

查看试题解析
17. 如图，在四边形 $A B C D$ 中，点E、F分别是线段AD、BC的中点，G、H分别是线段BD、AC的中点，当四边形 $A B C D$ 的边满足时，四边形 $E G F H$ 是菱形.

查看试题解析
18. 如图，正方形 $A B C D$ 的边长为4，对角线AC、BD相交于点O，点E在线段CD上，且 $C E = 3 D E$ ，过点C作 $C F ⊥ B E ，$ 垂足为点F.连接OF，则OF的长为.

查看试题解析

三、解答题

19. 约分:

(1)、 $\frac{12 x y}{18 x^{3} y^{2}}$

(2)、 $\frac{2 m - 8}{m^{2} - 16}$

查看试题解析
20. 计算:

(1)、 $\frac{b^{2}}{3 a} \cdot \frac{9 a^{2}}{2 b c}$ ；

(2)、 $\frac{12}{m^{2} - 9} - \frac{2}{3 - m}$

查看试题解析
21. 先化简，再求值： $(\frac{a^{2} - 5 a + 2}{a + 2} + 1) \div \frac{a^{2} - 4}{a^{2} + 4 a + 4}$ ，其中 $a = 3$ .

查看试题解析
22. 如图，在菱形ABCD中，对角线AC、BD相交于点O，过A作 $A E / / B D$ ，过D作 $D E / / A C ， A E$ 与DE相交于点E.求证：四边形AODE为矩形.

查看试题解析

23. 为弘扬中华传统文化，某校组织八年级8000名学生参加汉字听写大赛.为了解学生整体听写能力，从中抽取部分学生的成绩(得分取正整数，满分为100分)进行统计分析，得到如下所示的频数分布表：

分数段	$50.5 ~ 60.5$	$60.5 ~ 70.5$	$70.5 ~ 80.5$	$80.5 ~ 90.5$	$90.5 ~ 100.5$
频数	16	30	50	m	24
所占百分比	8%	15%	25%	40%	N%

请根据尚未完成的表格，解答下列问题：

(1)、本次抽样调查的样本容量为，表中m= ， n=；

(2)、补全如图所示的频数分布直方图；

(3)、若成绩超过80分为优秀，则该校八年级学生中汉字听写能力优秀的约有多少人？

查看试题解析

24. 在学习了“普查与抽样调查”之后，某校八（1）班数学兴趣小组对该校学生的视力情况进行了抽样调查，并画出了如图所示的条形统计图.请根据图中信息解决下列问题：

(1)、本次抽查活动中共抽查了名学生；

(2)、已知该校七年级、八年级、九年级学生数分别为360人、400人、540人.
①试估算：该校九年级视力不低于4.8的学生约有_▲_名；

②请你帮忙估算出该校视力低于4.8的学生数.

查看试题解析
25. 已知，如图在 $▱ A B C D$ 中， $A B = A C$ .

(1)、请用无刻度的直尺和圆规，画出 $△ A B C$ 中AB边上的中线CE；(作图要求：保留痕迹，不写作法.)

(2)、请只用无刻度的直尺，画出 $▱ A B C D$ 中BC边上的高AH，并说明理由.

查看试题解析
26. 已知： $l / / m / / n / / k ，$ 平行线l与m、m与n、n与k之间的距离分别为 $d_{1} ， d_{2} ， d_{3} ，$ 且 $d_{1}$ $= d_{3} = 2$ ， $d_{2} = 3$ .我们把四个顶点分别在l，m，n，k这四条平行线上的四边形称为“线上四边形”

(1)、如图1，正方形 $A B C D$ 为“线上四边形”， $B E ⊥ l$ 于点E，EB的延长线交直线k于点F.求正方形 $A B C D$ 的边长.

(2)、如图2，菱形ABCD为“线上四边形”且 $∠ A D C = 60 ° ， △ A E F$ 是等边三角形，点E在直线k上，连接DF，且DF的延长线分别交直线l、k于点G、M.求证： $E C = D F$ .

查看试题解析
27. 如图，在矩形 $A B C D$ 中， $A B = 2 ， A D = m$ ，动点P从点D出发，沿射线DA以每秒1个单位的速度向点A方向运动，连接CP，把 $△ P D C$ 沿PC翻折，得到 $△ P E C$ .设点P的运动时间为 $t (s)$ .

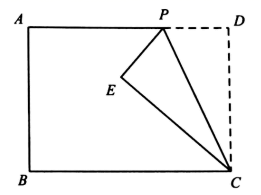(1)、若 $m = 3$ ，当P、E、B三点在同一直线上时，求t的值；

(2)、若点E到直线BC的距离等于1，求t的值；

(3)、若AE的最小值为1，直接写出m的值.

查看试题解析