江苏省南京市栖霞区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-06-08 类型:期中考试
一、选择题
-
1. 下面图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、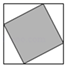 C、
C、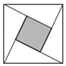 D、
D、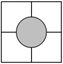 2. 下列调查中,适合普查方式的是( )A、调查某市初中生的睡眠情况 B、调查某班级学生的身高情况 C、调查南京秦淮河的水质情况 D、调查某品牌钢笔的使用寿命3. 为了解某校八年级320名学生的体重情况,从中抽查了80名学生的体重进行统计分析,以下说法正确的是( )A、320名学生的全体是总体 B、80名学生是总体的一个样本 C、每名学生的体重是个体 D、80名学生是样本容量4. 小明和同学做“抛掷质地均匀的硬币试验”,获得的数据如下表:
2. 下列调查中,适合普查方式的是( )A、调查某市初中生的睡眠情况 B、调查某班级学生的身高情况 C、调查南京秦淮河的水质情况 D、调查某品牌钢笔的使用寿命3. 为了解某校八年级320名学生的体重情况,从中抽查了80名学生的体重进行统计分析,以下说法正确的是( )A、320名学生的全体是总体 B、80名学生是总体的一个样本 C、每名学生的体重是个体 D、80名学生是样本容量4. 小明和同学做“抛掷质地均匀的硬币试验”,获得的数据如下表:抛掷次数
100
500
1000
1500
2000
正面朝上的频数
45
253
512
756
1020
若抛掷硬币的次数为3000,则“正面朝上”的频数最接近( )
A、1000 B、1500 C、2000 D、25005. 下列条件中,不能判定平行四边形ABCD为矩形的是( )A、∠A=∠C B、∠A=∠B C、AC=BD D、AB⊥BC6. 我们把顺次连接四边形各边中点所得的四边形叫做中点四边形.若一个任意四边形的面积为a,则它的中点四边形面积为( )A、 a B、 C、 D、二、填空题
-
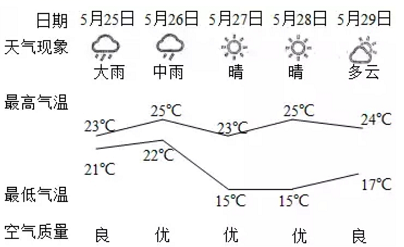
7. 在整数20200520中,数字“0”出现的频率是.8. 一个不透明的袋中装有3个红球,2个黑球,每个球除颜色外都相同.从中任意摸出3球,则“摸出的球至少有1个红球”是事件.(填“必然”、“不可能”或“随机”)9. 如图是某市连续5天的天气情况,最大的日温差是℃.
 10. 根据某商场2019年四个季度的营业额绘制成如图所示的扇形统计图,其中二季度的营业额为800万元,则该商场全年的营业额为万元.
10. 根据某商场2019年四个季度的营业额绘制成如图所示的扇形统计图,其中二季度的营业额为800万元,则该商场全年的营业额为万元. 11. 为了了解某校学生的视力情况,随机抽取了该校50名学生进行调查.整理样本数据如下表:
11. 为了了解某校学生的视力情况,随机抽取了该校50名学生进行调查.整理样本数据如下表:视力
4.7以下
4.7
4.8
4.9
4.9以上
人数
12
8
7
9
14
根据抽样调查结果,估计该校1 200名初中学生视力不低于4.8的人数是.
12. 如图,在平行四边形ABCD中,若∠A=2∠B,则∠D °.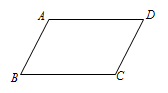 13. 如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=°.
13. 如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=°.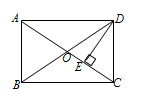 14. 如图,在菱形ABCD中,若AC=24 cm,BD=10 cm,则菱形ABCD的高为cm.
14. 如图,在菱形ABCD中,若AC=24 cm,BD=10 cm,则菱形ABCD的高为cm.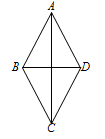 15. 如图,将△ABC绕点 旋转到△AEF的位置,点E在BC边上,EF与AC交于点G.若∠B=70°,∠C=25°,则∠FGC=°.
15. 如图,将△ABC绕点 旋转到△AEF的位置,点E在BC边上,EF与AC交于点G.若∠B=70°,∠C=25°,则∠FGC=°.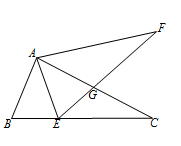 16. 如图,点E在正方形ABCD的边CD上,以CE为边向正方形ABCD外部作正方形CEFG,O、O′分别是两个正方形的对称中心,连接OO′.若AB=3,CE=1,则OO′=.
16. 如图,点E在正方形ABCD的边CD上,以CE为边向正方形ABCD外部作正方形CEFG,O、O′分别是两个正方形的对称中心,连接OO′.若AB=3,CE=1,则OO′=.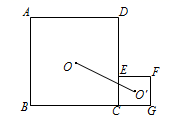
三、解答题
-
17. 如图,已知△ABC.
 (1)、画△ABC关于点C对称的△A′B′C;(2)、连接AB′、A′B,四边形ABA'B'是形.(填平行四边形、矩形、菱形或正方形)18. 某种油菜籽在相同条件下的发芽实验结果如下表:
(1)、画△ABC关于点C对称的△A′B′C;(2)、连接AB′、A′B,四边形ABA'B'是形.(填平行四边形、矩形、菱形或正方形)18. 某种油菜籽在相同条件下的发芽实验结果如下表:每批粒数n
100
150
200
500
800
1 000
发芽的粒数m
65
111
136
345
560
700
发芽的频率

0.65
0.74
0.68
0.69
a
b
(1)、a= , b=;(2)、这种油菜籽发芽的概率估计值是多少?请简要说明理由;(3)、如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10 000粒该种油菜籽可得到油菜秧苗多少棵?19. 某中学八年级共有10个班,每班40名学生,学校对该年级学生数学学科某次学情调研测试成绩进行了抽样分析,请按要求回答下列问题:(1)、若要从全年级学生中抽取40人进行调查,你认为以下抽样方法中最合理的是.①随机抽取一个班级的40名学生的成绩;
②在八年级学生中随机抽取40名女学生的成绩;
③在八年级10个班中每班各随机抽取4名学生的成绩.
(2)、将抽取的40名学生的成绩进行分组,绘制如下成绩频数分布表:①m=_▲_,n=_▲_;
②根据表格中的数据,请用扇形统计图表示学生成绩分布情况.
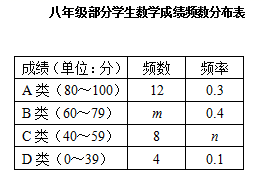 20. 为了解某区初中生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示不完整的统计图.
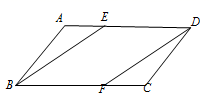
20. 为了解某区初中生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示不完整的统计图.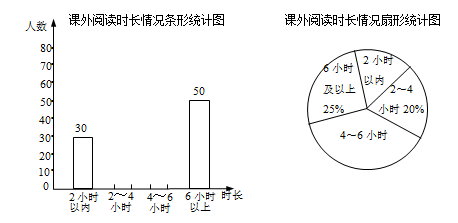 (1)、本次调查共随机抽取了名学生;(2)、补全条形统计图;(3)、扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 ,(4)、若该区共有10000名初中生,估计该地区中学生一周课外阅读时长不少于4小时的人数.21. 已知:如图,在¨ABCD中,点E、F分别在AD、BC上,且∠ABE=∠CDF.
(1)、本次调查共随机抽取了名学生;(2)、补全条形统计图;(3)、扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 ,(4)、若该区共有10000名初中生,估计该地区中学生一周课外阅读时长不少于4小时的人数.21. 已知:如图,在¨ABCD中,点E、F分别在AD、BC上,且∠ABE=∠CDF.求证:四边形BFDE是平行四边形.
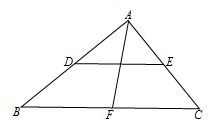
 22. 如图,在△ABC中,∠BAC=90°,DE是△ABC的中位线,AF是△ABC的中线.
22. 如图,在△ABC中,∠BAC=90°,DE是△ABC的中位线,AF是△ABC的中线.求证DE=AF.
 (1)、证法1:∵DE是△ABC的中位线,
(1)、证法1:∵DE是△ABC的中位线,∴DE=.
∵AF是△ABC的中线,∠BAC=90°,
∴AF= ,
∴DE=AF.
(2)、请把证法1补充完整,并用不同的方法完成证法2.证法2:
23. 如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F、H在菱形ABCD的对角线BD上.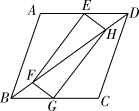 (1)、求证:BG=DE;(2)、若E为AD中点,FH=2,求菱形ABCD的周长。24. 如图,在矩形ABCD中,AB=1,BC=3.(1)、在图①中,P是BC上一点,EF垂直平分AP,分别交AD、BC边于点E、F,求证:四边形AFPE是菱形;(2)、在图②中利用直尺和圆规作出面积最大的菱形,使得菱形的四个顶点都在矩形ABCD的边上,并直接标出菱形的边长.(保留作图痕迹,不写作法)
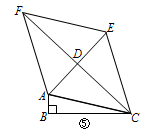
(1)、求证:BG=DE;(2)、若E为AD中点,FH=2,求菱形ABCD的周长。24. 如图,在矩形ABCD中,AB=1,BC=3.(1)、在图①中,P是BC上一点,EF垂直平分AP,分别交AD、BC边于点E、F,求证:四边形AFPE是菱形;(2)、在图②中利用直尺和圆规作出面积最大的菱形,使得菱形的四个顶点都在矩形ABCD的边上,并直接标出菱形的边长.(保留作图痕迹,不写作法)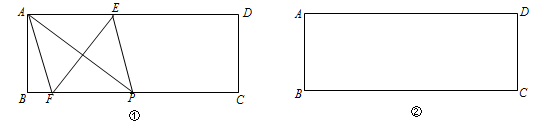 25. 如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
25. 如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.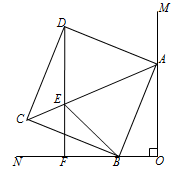 (1)、求证BE=DE;(2)、判断DF与ON的位置关系,并说明理由;(3)、△BEF的周长为.26. 定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.
(1)、求证BE=DE;(2)、判断DF与ON的位置关系,并说明理由;(3)、△BEF的周长为.26. 定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.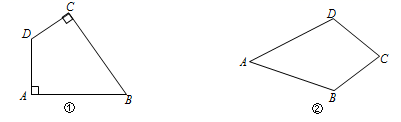 (1)、如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);
(1)、如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);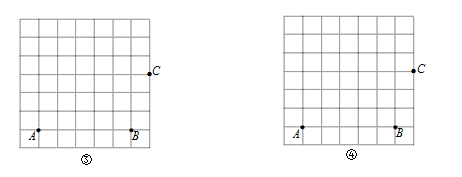 (2)、下列说法正确的有;(填写所有正确结论的序号)
(2)、下列说法正确的有;(填写所有正确结论的序号)①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;
③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.
(3)、如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;
②在①的条件下,连接BD,若BD=
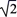 ,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.