广东省深圳市南山区2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-06-08 类型:期中考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列图形中的两个角互为补角的是( )


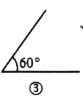
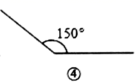 A、①和② B、①和③ C、①和④ D、③和④3. 生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子直径约为0.0000002cm,这个数量用科学记数法可表示为( )A、0.2×10-6cm B、2×10-6cm C、0.2×10-7cm D、2×10-7cm4. 如图,直线 与 相交于点 , 为 的角平分线,若 ,则 的度数为( )
A、①和② B、①和③ C、①和④ D、③和④3. 生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子直径约为0.0000002cm,这个数量用科学记数法可表示为( )A、0.2×10-6cm B、2×10-6cm C、0.2×10-7cm D、2×10-7cm4. 如图,直线 与 相交于点 , 为 的角平分线,若 ,则 的度数为( ) A、25° B、26° C、27° D、28°5. 如图,点P是直线a外一点,过点P作 于点A,在直线a上取一点B,连结PB,使 ,C在线段AB上,连结PC.若 ,则线段PC的长不可能是( )
A、25° B、26° C、27° D、28°5. 如图,点P是直线a外一点,过点P作 于点A,在直线a上取一点B,连结PB,使 ,C在线段AB上,连结PC.若 ,则线段PC的长不可能是( )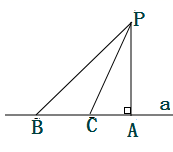 A、3.8 B、4.9 C、5.6 D、5.96. 纳米是一种长度单位,1米 纳米,已知某种植物花粉的直径约为45000纳米,那么科学记数法表示这种花粉的直径为( )A、 米 B、 米 C、 米 D、 米7. 不等式2x﹣4<0的解集是( )A、x<2 B、x>2 C、x≤2 D、x≥28. 如果 a<b , 那么下列不等式成立的是( )A、a﹣b>0 B、a﹣3>b﹣3 C、2a>2b D、﹣3a>﹣3b9. 下列语句中,假命题的是( )A、对顶角相等 B、若直线a、b、c满足b∥a,c∥a,那么b∥c C、两直线平行,同旁内角互补 D、互补的角是邻补角10. AF是 的平分线, 若 则 的度数为( )
A、3.8 B、4.9 C、5.6 D、5.96. 纳米是一种长度单位,1米 纳米,已知某种植物花粉的直径约为45000纳米,那么科学记数法表示这种花粉的直径为( )A、 米 B、 米 C、 米 D、 米7. 不等式2x﹣4<0的解集是( )A、x<2 B、x>2 C、x≤2 D、x≥28. 如果 a<b , 那么下列不等式成立的是( )A、a﹣b>0 B、a﹣3>b﹣3 C、2a>2b D、﹣3a>﹣3b9. 下列语句中,假命题的是( )A、对顶角相等 B、若直线a、b、c满足b∥a,c∥a,那么b∥c C、两直线平行,同旁内角互补 D、互补的角是邻补角10. AF是 的平分线, 若 则 的度数为( ) A、17.5° B、35° C、55° D、70°11. 如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点 处,点B落在点 处,若 则图中 的度数为( )
A、17.5° B、35° C、55° D、70°11. 如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点 处,点B落在点 处,若 则图中 的度数为( )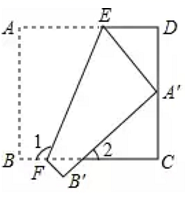 A、40° B、45° C、50° D、60°12. 如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是( )
A、40° B、45° C、50° D、60°12. 如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是( )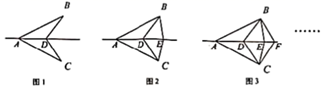 A、N B、2n-1 C、 D、3(n+1)
A、N B、2n-1 C、 D、3(n+1)二、填空题
-
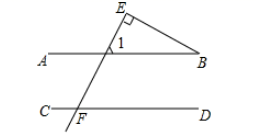
13. 是完全平方公式,则 .14. 如图, 于 , ,则 的度数是
 15. 现定义运算“△”,对于任意有理数a,b,都有a△b=a2﹣ab+b,
15. 现定义运算“△”,对于任意有理数a,b,都有a△b=a2﹣ab+b,例如:3△5=32﹣3×5+5=﹣1,由此算出(x﹣1)△(2+x)= 。
16. 初2021级某班班树现在高60厘米,以后每个月长高2厘米, 月后这棵树的高度为 厘米,则 与 的函数关系式为.17. 如图所示,为一个沙漏在计时过程中所剩沙子质量(克)与时间(小时)之间关系的图象,则从开始计时到沙子漏光所需的时间为小时.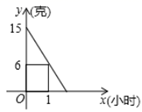 18. 如图,若直线 , , ,则 的度数为 .
18. 如图,若直线 , , ,则 的度数为 .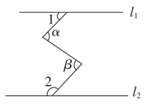
三、解答题
-
19. 计算下列各题:(1)、(2)、(3)、(4)、20. 先化简,再求值: ,其中 , .21. 如图,已知点 为 的边 上一点,请在边 上确定一点 ,使得 (要求:尺规做图、保留作图痕迹、不写作法)
 22. 星期五小颖放学步行从学校回家,当她走了一段路后,想起要去买彩笔做画报,于是原路返回到刚经过的文具用品店,买到彩笔后继续往家走.如图是她离家的距离与所用时间的关系示意图,请根据图中提供的信息回答下列问题:
22. 星期五小颖放学步行从学校回家,当她走了一段路后,想起要去买彩笔做画报,于是原路返回到刚经过的文具用品店,买到彩笔后继续往家走.如图是她离家的距离与所用时间的关系示意图,请根据图中提供的信息回答下列问题: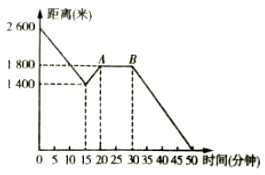 (1)、小颖家与学校的距离是米;(2)、 表示的实际意义是;(3)、小颖本次从学校回家的整个过程中,走的路程是多少米?(4)、买到彩笔后,小颖从文具用品店回到家步行的速度是多少米/分?23. 在学习“乘法公式“时,育红中学七(1)班数学兴趣小组在活动课上进行了这样的操作:作两条互相垂直的线段 和 ,把大正方形分成四部分(如图所示).
(1)、小颖家与学校的距离是米;(2)、 表示的实际意义是;(3)、小颖本次从学校回家的整个过程中,走的路程是多少米?(4)、买到彩笔后,小颖从文具用品店回到家步行的速度是多少米/分?23. 在学习“乘法公式“时,育红中学七(1)班数学兴趣小组在活动课上进行了这样的操作:作两条互相垂直的线段 和 ,把大正方形分成四部分(如图所示).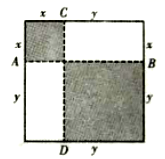 (1)、观察发现
(1)、观察发现请用两种不同的方法表示图形的面积,得到一个等量关系:
(2)、类比操作请你作一个图形验证: .
(3)、延伸运用若 ,如图中阴影部分的面积和为13,求 的值.
24. 已知,如图,把直角三角形 的直角顶点 放在直线 上,射线 平分 . (1)、如图,若 ,求 的度数.(2)、若 ,则 的度数为.(3)、由(1)和(2),我们发现 和 之间有什么样的数量关系?(4)、若将三角形 绕点 旋转到如图所示的位置,试问 和 之间的数量关系是否发生变化?请说明理由.
(1)、如图,若 ,求 的度数.(2)、若 ,则 的度数为.(3)、由(1)和(2),我们发现 和 之间有什么样的数量关系?(4)、若将三角形 绕点 旋转到如图所示的位置,试问 和 之间的数量关系是否发生变化?请说明理由.