广东省惠州市惠东县2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-06-08 类型:期中考试
一、单选题
-
1. 下列标志既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 则下列式子中错误的是( )A、 B、 C、 D、3. 不等式 的解集是( )A、 B、 C、 D、4. 已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )A、(1,2) B、(2,9) C、(5,3) D、(–9,–4)5.
2. 若 则下列式子中错误的是( )A、 B、 C、 D、3. 不等式 的解集是( )A、 B、 C、 D、4. 已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )A、(1,2) B、(2,9) C、(5,3) D、(–9,–4)5.如图,∠BAC=90°,AD⊥BC,∠BAD=30°,则∠C的度数是( )
 A、30° B、40° C、50° D、60°6. 在Rt△ABC中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于( )
A、30° B、40° C、50° D、60°6. 在Rt△ABC中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于( )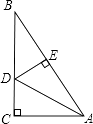 A、3.8cm B、7.6cm C、11.4cm D、11.2cm7. 如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路的距离相等,那么选择油库的位置有( )处.
A、3.8cm B、7.6cm C、11.4cm D、11.2cm7. 如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路的距离相等,那么选择油库的位置有( )处.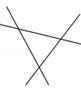 A、1 B、2 C、3 D、48. 关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )A、 B、 C、 D、9. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A , 则不等式0<kx+b<2x的解集为( )
A、1 B、2 C、3 D、48. 关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )A、 B、 C、 D、9. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A , 则不等式0<kx+b<2x的解集为( ) A、 B、 C、 D、10. 如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是( )秒
A、 B、 C、 D、10. 如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是( )秒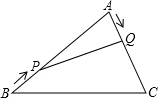 A、2.5 B、3 C、3.5 D、4
A、2.5 B、3 C、3.5 D、4二、填空题
-
11. 等腰三角形的一个外角是60°,则它的顶角的度数是 .12. 若 ,则 .13. 不等式组 ,的解集是 .14. 如图,将 沿 方向平移 得到 ,如果 的周长为 ,那么四边形 的周长为 .
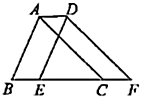 15. 如图,AC⊥BC于点C , DE⊥BE于点E , BC平分∠ABE , ∠BDE=58°,则∠A=°.
15. 如图,AC⊥BC于点C , DE⊥BE于点E , BC平分∠ABE , ∠BDE=58°,则∠A=°. 16.
16.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
 17. 已知一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;正确的说法有 . (请写出所有正确说法的序号)
17. 已知一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;正确的说法有 . (请写出所有正确说法的序号)三、解答题
-
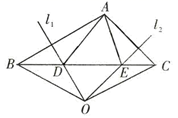
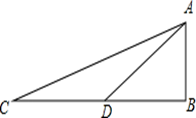
18. 如图:在△ABC中,∠B=90°,AB=BD,AD=CD,求∠CAD的度数.
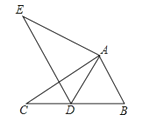
 19. 如图,已知AD平分△ABC的外角∠EAC,且∠EAD=∠C,求证:AB=AC.
19. 如图,已知AD平分△ABC的外角∠EAC,且∠EAD=∠C,求证:AB=AC. 20. 如图,已知:在 中, , .
20. 如图,已知:在 中, , .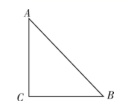 (1)、按下列步骤用尺规作图(保留作图痕迹,不写出作法):作 的平分线AD,交BC于D;(2)、在(1)中,过点D作 ,交AB于点E,若CD=4,则BC的长为 .21. 若关于 的方程组 的解满足 ,求 的取值范围.22. 如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).三角形AOB中任意一点 经平移后的对应点为 ,并且点A,O,B的对应点分别为点D,E,F.
(1)、按下列步骤用尺规作图(保留作图痕迹,不写出作法):作 的平分线AD,交BC于D;(2)、在(1)中,过点D作 ,交AB于点E,若CD=4,则BC的长为 .21. 若关于 的方程组 的解满足 ,求 的取值范围.22. 如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).三角形AOB中任意一点 经平移后的对应点为 ,并且点A,O,B的对应点分别为点D,E,F. (1)、画出平移后的三角形DEF并标出D,E,F点的坐标;(2)、求线段OA在平移过程中扫过的面积.23. 为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.(1)、求足球和篮球的单价各是多少元?(2)、根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
(1)、画出平移后的三角形DEF并标出D,E,F点的坐标;(2)、求线段OA在平移过程中扫过的面积.23. 为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.(1)、求足球和篮球的单价各是多少元?(2)、根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?