广东省广州市越秀区培正学院2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-06-08 类型:期中考试
一、单选题
-
1. 使 有意义的x的取值范围是( )
A、x≤3 B、x<3 C、x≥3 D、x>32. 下列命题中,错误的是( ).A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直平分 C、矩形的对角线相等且互相垂直平分 D、角平分线上的点到角两边的距离相等3. 下列二次根式中的最简二次根式是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、( )﹣1= C、 = ﹣2 D、 =±35. 五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )A、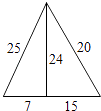 B、
B、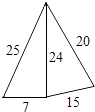 C、
C、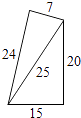 D、
D、 6. 如图,在菱形ABCD中,AB=10,两条对角线相交于点O , 若OB=6,则菱形面积是( )
6. 如图,在菱形ABCD中,AB=10,两条对角线相交于点O , 若OB=6,则菱形面积是( ) A、60 B、48 C、24 D、967. 如图,平行四边形ABCD的对角线AC、BD相较于点O,EF过点O,且与AD、BC分别相交于E、F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长是( )
A、60 B、48 C、24 D、967. 如图,平行四边形ABCD的对角线AC、BD相较于点O,EF过点O,且与AD、BC分别相交于E、F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长是( ) A、16 B、14 C、12 D、108. 实数a、b满足 +4a2+4ab+b2=0,则ba的值为( )A、2 B、 C、﹣2 D、﹣9. 若x+y=3+2 ,x﹣y=3﹣2 ,则 的值为( )A、4 B、1 C、6 D、3﹣210. 如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为( )
A、16 B、14 C、12 D、108. 实数a、b满足 +4a2+4ab+b2=0,则ba的值为( )A、2 B、 C、﹣2 D、﹣9. 若x+y=3+2 ,x﹣y=3﹣2 ,则 的值为( )A、4 B、1 C、6 D、3﹣210. 如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为( ) A、10 B、12 C、16 D、18
A、10 B、12 C、16 D、18二、填空题
-
11. 如果实数a、b在数轴上的位置如图所示,那么化简 = .
 12. 如图,在等腰三角形ABC中,AB=AC , D , E分别是AB , AC的中点,若∠A=20°,则∠ADE= .
12. 如图,在等腰三角形ABC中,AB=AC , D , E分别是AB , AC的中点,若∠A=20°,则∠ADE= . 13. 若 =3-x,则x的取值范围是 .14. 在▱ABCD中,AB:BC=4:3,周长为28cm,则AD=cm.15.
13. 若 =3-x,则x的取值范围是 .14. 在▱ABCD中,AB:BC=4:3,周长为28cm,则AD=cm.15.如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为 .
 16. 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.
16. 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.
三、解答题
-
17. 计算:(1)、 .(2)、 .(3)、 .18. 已知:矩形ABCD的一条对角线AC长8,两条对角线的一个交角∠AOB=60°,求这个矩形的面积.
 19. 如图,每个小正方形的边长为1.
19. 如图,每个小正方形的边长为1. (1)、求BC与CD的长;(2)、求证:∠BCD=90°.20. 如图,在平面直角坐标系中,将矩形ABCD沿直线AE折叠(点E在边DC上),折叠后顶点恰好落在边OC上的点F处,若点D的坐标为(10,8).
(1)、求BC与CD的长;(2)、求证:∠BCD=90°.20. 如图,在平面直角坐标系中,将矩形ABCD沿直线AE折叠(点E在边DC上),折叠后顶点恰好落在边OC上的点F处,若点D的坐标为(10,8).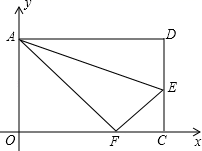 (1)、求CE的长;(2)、写出点E的坐标.21. 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
(1)、求CE的长;(2)、写出点E的坐标.21. 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).
 (1)、作∠DAC的平分线AM;(2)、作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
(1)、作∠DAC的平分线AM;(2)、作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.猜想并证明:判断四边形AECF的形状并加以证明.
22.(1)、操作发现:如图①,小明画了一个等腰三角形ABC , 其中AB=AC , 在△ABC的外侧分别以AB , AC为腰作了两个等腰直角三角形ABD , ACE , 分别取BD , CE , BC的中点M , N , G , 连接GM , GN . 小明发现了:线段GM与GN的数量关系是;位置关系是 .(2)、类比思考:如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC , 其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)、深入研究:如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD , ACE , 其它条件不变,试判断△GMN的形状,并给与证明.
 23. 如图,在正方形 中, 是边 上的一动点(不与点 , 重合),连接 ,点 关于直线 的对称点为 ,连接 并延长交 于点 ,连接 ,过点 作 交 的延长线于点 ,连接 .
23. 如图,在正方形 中, 是边 上的一动点(不与点 , 重合),连接 ,点 关于直线 的对称点为 ,连接 并延长交 于点 ,连接 ,过点 作 交 的延长线于点 ,连接 .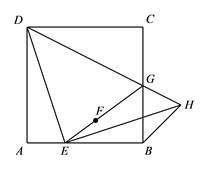 (1)、求证: ;
(1)、求证: ;
(2)、用等式表示线段 与 的数量关系,并证明.