山西省运城市盐湖区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-08 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列各式由左到右的变形中，属于分解因式的是（）

A、 $a (m + n) = a m + a n$ B、 $a^{2} - b^{2} - c^{2} = (a + b) (a - b) - c^{2}$ C、 $10 x^{2} - 5 x = 5 x (2 x - 1)$ D、 $x - 16 + 8 x = (x + 4) (x - 4) + 8 x$

查看试题解析
3. 不等式5+2x ＜1的解集在数轴上表示正确的是（）.

A、 B、 C、 D、

查看试题解析
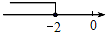4. 已知一个多边形的内角和是360°，则这个多边形是（）

A、四边形 B、五边形 C、六边形 D、七边形

查看试题解析
5. 要使分式 $\frac{1}{x - 2}$ 有意义，则x 的取值应满足（）

A、x =2 B、x ＜2 C、x ＞2 D、x ≠2

查看试题解析
6. 如图，若平行四边形ABCD的周长为40cm，BC＝ $\frac{2}{3}$ AB，则BC＝（）

A、16crn B、14cm C、12cm D、8cm

查看试题解析
7. 若关于x的方程 $\frac{x + m}{x - 3}$ + $\frac{3 m}{3 - x}$ =3的解为正数，则m的取值范围是（）

A、m＜ $\frac{9}{2}$ B、m＜ $\frac{9}{2}$ 且m≠ $\frac{3}{2}$ C、m＞﹣ $\frac{9}{4}$ D、m＞﹣ $\frac{9}{4}$ 且m≠﹣ $\frac{3}{4}$

查看试题解析
8. 如图，将一个含 $30^{\circ}$ 角的直角三角板 $A B C$ 绕点 $A$ 旋转，得点 $B$ ， $A$ ， $C'$ ，在同一条直线上，则旋转角 $∠ B A B'$ 的度数是（）

A、 $60^{\circ}$ B、 $90^{\circ}$ C、 $120^{\circ}$ D、 $150^{\circ}$

查看试题解析
9. 如图， $Δ A B C$ 中， $A B = A C = 15$ ， $A D$ 平分 $∠ B A C$ ，点 $E$ 为 $A C$ 的中点，连接 $D E$ ，若 $Δ C D E$ 的周长为24，则 $B C$ 的长为（）

A、18 B、14 C、12 D、6

查看试题解析
10. 定义一种新运算：当 $a > b$ 时， $a \oplus b = a b + b$ ；当 $a < b$ 时， $a \oplus b = a b - b$ .若 $3 \oplus (x + 2) > 0$ ，则 $x$ 的取值范围是（）

A、 $- 1 < x < 1$ 或 $x < - 2$ B、 $x < - 2$ 或 $1 < x < 2$ C、 $- 2 < x < 1$ 或 $x > 1$ D、 $x < - 2$ 或 $x > 2$

查看试题解析

二、填空题

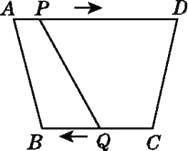
11. 在平面直角坐标系中，点 $(2, - 3)$ 关于 $x$ 轴对称的点的坐标是．

查看试题解析
12. 若a²﹣5ab﹣b²＝0，则 $\frac{a}{b} - \frac{b}{a}$ 的值为．

查看试题解析
13. 如图，在四边形ABCD中，AD∥BC，且AD>BC，BC=6 cm，动点P，Q分别从A，C同时出发，P以1 cm/s的速度由A向D运动，Q以2 cm/s的速度由C向B运动(Q运动到B时两点同时停止运动)，则后四边形ABQP为平行四边形.

查看试题解析
14. 在代数式 $\frac{5}{3 a}$ ， $\frac{7}{10}$ ， $\frac{2}{2 b - 1}$ ， $\frac{y - 1}{2}$ ， $x + \frac{y}{8}$ 中，是分式的有个.

查看试题解析
15. 如图，分别以 $R t Δ A B C$ 的斜边 $A B$ ，直角边 $A C$ 为边向外作等边 $Δ A B D$ 和 $Δ A C E$ ， $F$ 为 $A B$ 的中点， $D E$ ， $A B$ 相交于点 $G$ .若∠BAC=30°，下列结论：① $E F ⊥ A C$ ；②四边形 $A D F E$ 为平行四边形；③ $A D = 4 A G$ ；④ $Δ D B F ≅ Δ E F A$ .其中正确结论的序号是.

查看试题解析

三、综合题

16. 分解因式：

(1)、 $a^{2} x^{2} y - a x y^{2}$

(2)、 $a^{2} (x - y) + b^{2} (y - x)$

查看试题解析
17.

(1)、化简求值： $(\frac{2 m}{m + 3} - \frac{m}{m + 3}) \div \frac{m}{m^{2} - 9}$ ，其中 $m = - 1$ .

(2)、解不等式组： ${\begin{array}{l} 3 x - (x - 2) > 4 \\ \frac{2 x + 1}{3} > x - 1 \end{array}$ ，并把它的解集在数轴上表示出来.

查看试题解析
18. 已知：如图，平行四边形ABCD中，E、F分别是边BC和AD上的点，且BE=DF，

求证：AE=CF

查看试题解析
19. 在平面直角坐标系中， $Δ A B C$ 的位置如图所示（每个小方格都是边长1个单位长度的正方形）.

(1)、将 $Δ A B C$ 沿 $x$ 轴方向向左平移6个单位，画出平移后得到的 $Δ A_{1} B_{1} C_{1}$ .

(2)、将 $Δ A B C$ 绕着点 $A$ 顺时针旋转 $90^{\circ}$ ，画出旋转后得到的 $Δ A B_{2} C_{2}$ ；直接写出点 $B_{2}$ 的坐标.

(3)、作出 $Δ A B C$ 关于原点 $O$ 成中心对称的 $Δ A_{3} B_{3} C_{3}$ ，并直接写出 $B_{3}$ 的坐标.

查看试题解析
20. 探索发现： $\frac{1}{1 \times 2}$ =1﹣ $\frac{1}{2}$ ； $\frac{1}{2 \times 3}$ = $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ； $\frac{1}{3 \times 4}$ = $\frac{1}{3}$ ﹣ $\frac{1}{4}$ …
根据你发现的规律，回答下列问题：

(1)、 $\frac{1}{4 \times 5}$ = ， $\frac{1}{n \times (n + 1)}$ =；

(2)、利用你发现的规律计算： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{n \times (n + 1)}$

(3)、灵活利用规律解方程： $\frac{1}{x (x + 2)}$ + $\frac{1}{(x + 2) (x + 4)}$ +…+ $\frac{1}{(x + 98) (x + 100)}$ = $\frac{1}{x + 100}$ ．

查看试题解析
21. 如图， $D E$ 是 $Δ A B C$ 的中位线，过点 $C$ 作 $C F ∥ B D$ 交 $D E$ 的延长线于点 $F$ ，求证： $D E = F E$ .

查看试题解析
22. 运城市某学校去年在某商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.

(1)、求购买一个甲种足球、一个乙种足球各需多少元；

(2)、今年为响应习总书记“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了 $10 %$ ，乙种足球售价比第一次购买时降低了 $10 %$ .如果此次购买甲、乙两种足球的总费用不超过3000元，那么这所学校最多可购买多少个乙种足球？

查看试题解析
23. 在 $Δ A B C$ 中， $A B = A C$ ，点 $P$ 为 $Δ A B C$ 所在平面内一点，过点 $P$ 分别作 $P E ∥ A C$ 交 $A B$ 于点 $E$ ， $P F ∥ A B$ 交 $B C$ 于点 $D$ ，交 $A C$ 于点 $F$ .

若点 $P$ 在 $B C$ 上（如图①），此时 $P D = 0$ ，可得结论： $P D + P E + P F = A B$ .

请应用上述信息解决下列问题：

当点 $P$ 分别在 $Δ A B C$ 内（如图②）， $Δ A B C$ 外（如图③）时，上述结论是否成立？若成立，请给予证明；若不成立， $P D$ ， $P E$ ， $P F$ ，与 $A B$ 之间又有怎样的数量关系，请写出你的猜想，不需要证明.

查看试题解析