山西省大同市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-08 类型:期末考试
一、选择题
-
1. 下列各式计算正确的是( )A、 B、 C、 D、2. 若点A(2,3)在函数y=kx的图象上,则下列各点在此丽数图象上的是( )A、(1, ) B、(2,-3) C、(4,5) D、(-2,3)3. 下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )A、1,2,3 B、4,6,8 C、6,8,10 D、13,14,154. 如图,以原点O为圆心,OB长为半径画弧与数轴交于点A,若点A表示的数为x , 则x的值为( )
 A、 B、- C、 -2 D、2-5. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差s2:
A、 B、- C、 -2 D、2-5. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差s2:甲
乙
丙
丁
平均数 (cm)
561
560
561
560
方差s2(cm2)
3.5
3.5
15.5
16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择 .
6. 一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( ) A、x>0 B、x<0 C、x>-1 D、x>27. 如图是我国一位古代数学家在注解《周髀算经》时给出的,曾被选为2002年在北京召开的国际数学家大会的会徽,它通过对图形的切割、拼接,巧妙地证明了勾股定理,这位伟大的数学家是( )
A、x>0 B、x<0 C、x>-1 D、x>27. 如图是我国一位古代数学家在注解《周髀算经》时给出的,曾被选为2002年在北京召开的国际数学家大会的会徽,它通过对图形的切割、拼接,巧妙地证明了勾股定理,这位伟大的数学家是( ) A、杨辉 B、刘徽 C、祖冲之 D、赵爽8. 小明用作图象的方法解二元一次方程组时,他作出了相应的两个一次函数的图象,则他解的这个方程组是( )
A、杨辉 B、刘徽 C、祖冲之 D、赵爽8. 小明用作图象的方法解二元一次方程组时,他作出了相应的两个一次函数的图象,则他解的这个方程组是( ) A、 B、 C、 D、9. 已知将直线y=x+1向下平移3个单位长度后得到直线y=kx+b , 则下列关于直线y=kx+b的说法正确的是( )A、经过第一、二、四象限 B、与x轴交于(2,0) C、与直线y=2x+1平行 D、y随的增大而减小10. 如图,矩形 中, , ,点 从点 出发,沿 向终点 匀速运动.设点 走过的路程为 , 的面积为 ,能符合题意反映 与 之间函数关系的图象是( )
A、 B、 C、 D、9. 已知将直线y=x+1向下平移3个单位长度后得到直线y=kx+b , 则下列关于直线y=kx+b的说法正确的是( )A、经过第一、二、四象限 B、与x轴交于(2,0) C、与直线y=2x+1平行 D、y随的增大而减小10. 如图,矩形 中, , ,点 从点 出发,沿 向终点 匀速运动.设点 走过的路程为 , 的面积为 ,能符合题意反映 与 之间函数关系的图象是( )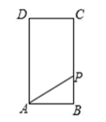 A、
A、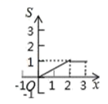 B、
B、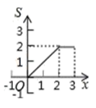 C、
C、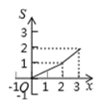 D、
D、
二、填空题
-
11. 函数 中自变量x的取值范围是.12. 如图,直线y=kx+b与直线y=2x交于点P(1,m),则不等式2x<kx+b的解集为.
 13. 如果两个最简二次根式 与 能合并,那么 .14. 如图,菱形ABCD中,AC、BD交于点O,DE⊥BC于点E,连接OE,若∠ABC=120°,则∠OED=.
13. 如果两个最简二次根式 与 能合并,那么 .14. 如图,菱形ABCD中,AC、BD交于点O,DE⊥BC于点E,连接OE,若∠ABC=120°,则∠OED=. 15. 如图,三个边长均为1的正方形按如图所示的方式摆放,A1 , A2分别是正方形对角线的交点,则重叠部分的面积和为.
15. 如图,三个边长均为1的正方形按如图所示的方式摆放,A1 , A2分别是正方形对角线的交点,则重叠部分的面积和为.
三、综合题
-
16. 计算:(1)、(1- )+|1-2 |+ × .(2)、( +2 )÷ - .17. 如图,在 ABCD中,延长边BA到点E,延长边DC到点F,使CF=AE,连接EF,分别交AD,BC于点M,N.
求证:AM=CN.
 18. 如图,正比例函数y1=kx与-次函数y2=mx+n的图象交于点A(3,4),一次函数y2的图象与x轴,y轴分别交于点B,点C,且0A=OC.
18. 如图,正比例函数y1=kx与-次函数y2=mx+n的图象交于点A(3,4),一次函数y2的图象与x轴,y轴分别交于点B,点C,且0A=OC. (1)、求这两个函数的解析式;(2)、求直线AB与两坐标轴所围成的三角形的面积.19. 随着教育教学改革的不断深入,应试教育向素质教育转轨的力度不断加大,体育中考已成为初中毕业升学考试的重要内容之一。为了解某市九年级学生中考体育成绩情况,现从中随机抽取部分考生的体育成绩进行调查,并将调查结果绘制如下图表:
(1)、求这两个函数的解析式;(2)、求直线AB与两坐标轴所围成的三角形的面积.19. 随着教育教学改革的不断深入,应试教育向素质教育转轨的力度不断加大,体育中考已成为初中毕业升学考试的重要内容之一。为了解某市九年级学生中考体育成绩情况,现从中随机抽取部分考生的体育成绩进行调查,并将调查结果绘制如下图表:2019年中考体育成绩(分数段)统计表
分数段
频数(人)
频率
25≤x<30
12
0.05
30≤x<35
24
b
35≤x<40
60
0.25
40≤x<45
a
0.45
45≤x<50
36
0.15

根据上面提供的信息,回答下列问题:
(1)、表中a和b所表示的数分别为a= , b=;并补全频数分布直方图;(2)、甲同学说“我的体育成绩是此次抽样调查所得数据的中位数。”请问:甲同学的体育成绩在分数段内?(3)、如果把成绩在40分以上(含40分)定为优秀那么该市12000名九年级考生中考体育成绩为优秀的约有多少名?20. 阅读下列一段文字,然后回答下列问题:已知平面内两点P1(x1 , y1),P2(x2 , y2),其两点间的距离 。例如:已知P(3,1),Q(1,-2),则这两点间的距离 .特别地,如果两点M(x1 , y1),N(x2 , y2),所在的直线与坐标轴重合或平行于坐标轴或者垂直于坐标轴,那么这两点间的距离公式可简化为 或 。
 (1)、已知A(2,3),B(-1,-2),则A,B两点间的距离为;(2)、已知M,N在平行于y轴的直线上,点M的纵坐标为-2,点N的纵坐标为3,则M,N两点间的距离为;(3)、在平面直角坐标系中,已知A(0,4),B(4,2),在x轴上找点P,使PA+PB的长度最短,求出点P的坐标及PA+PB的最短长度.21. “雁门清高”苦荞茶,是大同左云的特产,享誉全国,某经销商计划购进甲、乙两种包装的苦荞茶500盒进行销售,这两种茶的进价、售价如下表所示:
(1)、已知A(2,3),B(-1,-2),则A,B两点间的距离为;(2)、已知M,N在平行于y轴的直线上,点M的纵坐标为-2,点N的纵坐标为3,则M,N两点间的距离为;(3)、在平面直角坐标系中,已知A(0,4),B(4,2),在x轴上找点P,使PA+PB的长度最短,求出点P的坐标及PA+PB的最短长度.21. “雁门清高”苦荞茶,是大同左云的特产,享誉全国,某经销商计划购进甲、乙两种包装的苦荞茶500盒进行销售,这两种茶的进价、售价如下表所示:进价(元/盒)
售价(元/盒)
甲种
40
48
乙种
106
128
设该经销离购进甲种包装的苦荞茶x盒,总进价为y元。
(1)、求y与x的函数关系式(2)、为满足市场需求,乙种包装苦荞茶的数量不大于甲种包装数量的4倍,请你求出获利最大的进货方案,并求出最大利润。22. 综合与实践(问题情境)
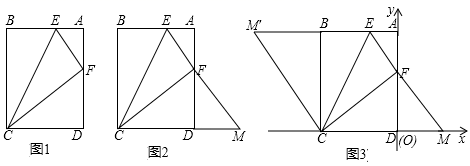
在综合与实践课上,同学们以“矩形的折叠”为主题展开数学活动,如图1,在矩形纸片ABCD中,AB=4,BC=5,点E,F分别为边AB,AD上的点,且DF=3。
(操作发现)
(1)、沿CE折叠纸片,B点恰好与F点重合,求AE的长;(2)、如图2,延长EF交CD的延长线于点M,请判断△CEM的形状,并说明理由。(3)、(深入思考)把图2置于平面直角坐标系中,如图3,使D点与原点O重合,C点在x轴的负半轴上,将△CEM沿CE翻折,使点M落在点M′处.连接CM′,求点M′的坐标.
23. 综合与探究如图,在平面直角坐标系中,直线y= x-3与坐标轴交于A,B两点.
 (1)、求A,B两点的坐标;(2)、以AB为边在第四象限内作等边三角形ABC,求△ABC的面积;(3)、在平面内是否存在点M,使得以M,O,A,B为顶点的四边形是平行四边形,若存在,直接写出M点的坐标:若不存在,说明理由.
(1)、求A,B两点的坐标;(2)、以AB为边在第四象限内作等边三角形ABC,求△ABC的面积;(3)、在平面内是否存在点M,使得以M,O,A,B为顶点的四边形是平行四边形,若存在,直接写出M点的坐标:若不存在,说明理由.