内蒙古巴彦淖尔市临河区八校联盟2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-08 类型：期末考试

进入出卷网下载

一、选择题

1. 若 $\sqrt{2 m - 3}$ 有意义，则m能取的最小整数值是（）

A、 $m = 0$ B、 $m = 1$ C、 $m = 2$ D、 $m = 3$

查看试题解析
2. 下列各组数中，以它们为边长的线段不能构成直角三角形的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、3，4，5 C、5，12，13 D、2，2，3

查看试题解析
3. 下列二次根式中属于最简二次根式的是（）

A、 $\sqrt{14}$ B、 $\sqrt{32}$ C、 $\sqrt{\frac{a}{b}}$ D、 $\sqrt{4 a + 4}$

查看试题解析
4. 函数y=2x﹣5的图象经过（）

A、第一、三、四象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、二、三象限

查看试题解析
5. 如图，矩形 $A B C D$ 中，对角线 $A C 、 B D$ 交于点 $O$ .若 $∠ A O B = 60^{\circ} ， B D = 8$ ，则 $A B$ 的长为（）

A、 $3$ B、 $4$ C、 $4 \sqrt{3}$ D、 $5$

查看试题解析
6. 如图，正方形ABCD中，AE垂直于BE，且AE＝3，BE＝4，则阴影部分的面积是（）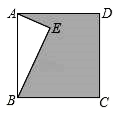

A、16 B、18 C、19 D、21

查看试题解析
7. 已知P₁（﹣3，y₁），P₂（2，y₂）是一次函数y=﹣x﹣1的图象上的两个点，则y₁ ， y₂的大小关系是（）

A、y₁=y₂ B、y₁＜y₂ C、y₁_＞y₂ D、不能确定

查看试题解析
8. 某市一周日最高气温如图所示，则该市这周的日最高气温的众数是（）

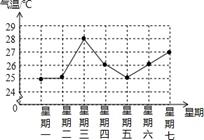A、25 B、26 C、27 D、28

查看试题解析

9. 2022年将在北京-张家口举办冬季奥运会，很多学校开设了相关的课程．如表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差

s^{2}

：

	队员1	队员2	队员3	队员4
平均数 $\bar{x}$ (秒)	51	50	51	50
方差 $s^{2}$ (秒²)	3.5	3.5	14.5	15.5

根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（）

A、队员1 B、队员2 C、队员3 D、队员4

查看试题解析

10. 如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，若BF=12，AB=10，则AE的长为（）

A、13 B、14 C、15 D、16

查看试题解析
11. 如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为（）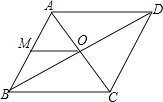

A、5cm B、10cm C、20cm D、40cm

查看试题解析
12. 一次函数 $y_{1} = k x + b$ 与 $y_{2} = x + a$ 的图象如图所示，给出下列结论：① $k < 0$ ；② $a > 0$ ；③当 $x < 3$ 时， $y_{1} < y_{2}$ .其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

13. 已知一组数据6、4、a、3、2的平均数是5，则a的值为．

查看试题解析
14. 将函数 $y = 3 x$ 的图象向下平移2个单位，所得函数图象的解析式为．

查看试题解析
15. $\sqrt{17}$ 的小数部分为．

查看试题解析
16. 如图所示，已知 $▱$ ABCD中，下列条件：①AC=BD；②AB=AD；③∠1=∠2；④AB⊥BC中，能说明 $▱$ ABCD是矩形的有（填写序号）

查看试题解析
17. 如图，直线y=kx+b（k≠0）与x轴交于点（﹣4，0），则关于x的方程kx+b=0的解为x= ．

查看试题解析
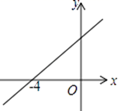18.
如图，矩形纸片ABCD的边长AB＝4，AD＝2，将矩形纸片沿EF折叠，使点A与点C重合，折叠后在其一面着色(如图)，着色部分的面积为.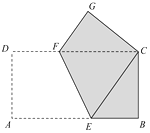

查看试题解析

三、综合题

19. 计算： $| 1 - \sqrt{3} | + {(\sqrt{3} - π)}^{0} + \sqrt[3]{64} - \sqrt{24} \div \sqrt{2}$

查看试题解析
20. 某高中学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准，共分为6种型号).

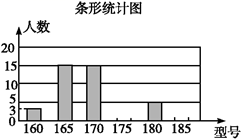
根据以上信息，解答下列问题：

(1)、该班共有名学生?其中穿175型校服的学生有人.

(2)、在条形统计图中，请把空缺的部分补充完整；

(3)、在扇形统计图中，请计算185型校服所对应扇形圆心角度数为；

(4)、该班学生所穿校服型号的众数是，中位数是.

查看试题解析
21. 已知，如图，E、F分别为▱ABCD的边BC、AD上的点，且∠1=∠2，.求证：AE=CF.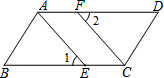

查看试题解析
22. 如图1，在△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交CE的延长线于F ，且AF＝BD ，连接BF ．

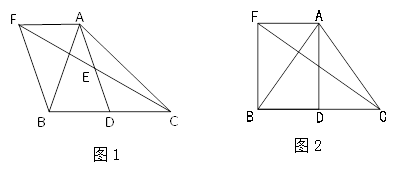(1)、求证：点D是线段BC的中点；

(2)、如图2，若AB＝AC=13， AF＝BD=5，求四边形AFBD的面积．

查看试题解析
23. 某经销商从市场得知如下信息：
A品牌手表
B品牌手表
进价（元/块）
700
100
售价（元/块）
900
160
他计划用4万元资金一次性购进这两种品牌手表共100块，设该经销商购进A品牌手表x块，这两种品牌手表全部销售完后获得利润为y元．

(1)、试写出y与x之间的函数关系式；

(2)、若要求全部销售完后获得的利润不少于1.26万元，该经销商有哪几种进货方案？

(3)、选择哪种进货方案，该经销商可获利最大？最大利润是多少元？

查看试题解析
24. 如图，在平面直角坐标系中，直线l₁： y= $- \frac{1}{2}$ x+6 分别与x轴、y轴交于点B、C，且与直线l₂： $y = \fra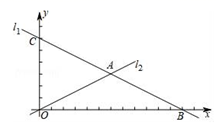c{1}{2} x$ 交于点A．

(1)、求出点A的坐标

(2)、若D是线段OA上的点，且△COD的面积为12，求直线CD的解析式

(3)、在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点P的坐标；若不存在，请说明理由．

查看试题解析

	A品牌手表	B品牌手表
进价（元/块）	700	100
售价（元/块）	900	160