山西省太原市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-06-08 类型:期末考试
一、选择题
-
1. 计算 的结果为( )A、 B、 C、 D、2. 2019年4月28日,北京世界园艺博览会正式开幕,在此之前,我国已举办过七次不同类别的世界园艺博览会.下面是北京、西安、锦州、沈阳四个城市举办的世园会的标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 小明连续抛一枚质量均匀的硬币 次,都是正面朝上,若他再抛一次,则朝上的一面( )A、一定是正面 B、是正面的可能性较大 C、一定是反面 D、是正面或反面的可能性一样大4. 如图,点 分别在 的边 上,点 在 的内部,若 ,则 的度数是( )
3. 小明连续抛一枚质量均匀的硬币 次,都是正面朝上,若他再抛一次,则朝上的一面( )A、一定是正面 B、是正面的可能性较大 C、一定是反面 D、是正面或反面的可能性一样大4. 如图,点 分别在 的边 上,点 在 的内部,若 ,则 的度数是( ) A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 据5月23日“人民日报”微信公众号文章介绍,中国兵器工业集团豫西集团中南钻石公司推出大颗粒“首饰用钻石”,打破了国外垄断,使我国在钻石饰品主流领域领跑全球,钻石、珠宝等宝石的质量单位是克拉( ), 克拉为 分,已知 克拉 克,则“ 分”用科学记数法表示正确的是( )
A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 据5月23日“人民日报”微信公众号文章介绍,中国兵器工业集团豫西集团中南钻石公司推出大颗粒“首饰用钻石”,打破了国外垄断,使我国在钻石饰品主流领域领跑全球,钻石、珠宝等宝石的质量单位是克拉( ), 克拉为 分,已知 克拉 克,则“ 分”用科学记数法表示正确的是( ) A、 克 B、 克 C、 克 D、 克7. 如图,点 在直线上, 与 关于直线 对称,连接 分别交 于点 连接 ,下列结论不一定正确的是( )
A、 克 B、 克 C、 克 D、 克7. 如图,点 在直线上, 与 关于直线 对称,连接 分别交 于点 连接 ,下列结论不一定正确的是( ) A、 B、 C、 D、8. 如图,一辆汽车在龙城大街上沿东向西方向正常行驶,从点 处开始减速驶入路况良好的祥云桥北匝道桥,接着驶入滨河东路后沿北向南继续正常行驶.下列四个图像中能刻画该汽车这个过程中行驶速度 (千米/时)与行驶时间 (时)之间的关系是( )
A、 B、 C、 D、8. 如图,一辆汽车在龙城大街上沿东向西方向正常行驶,从点 处开始减速驶入路况良好的祥云桥北匝道桥,接着驶入滨河东路后沿北向南继续正常行驶.下列四个图像中能刻画该汽车这个过程中行驶速度 (千米/时)与行驶时间 (时)之间的关系是( ) A、
A、 B、
B、 C、
C、 D、
D、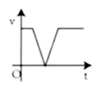 9. 如图, ,点 在边 上,线段 , 交于点 ,若 ,则 的度数为( )
9. 如图, ,点 在边 上,线段 , 交于点 ,若 ,则 的度数为( ) A、 B、 C、 D、10. 有一种手持烟花,点然后每隔 1.4 秒发射一发花弹。要求每一发花弹爆炸时的高度要超过 15 米,否则视为不合格,在一次测试实验中,该烟花发射出的第一发花弹的飞行高度(米)随飞行时间(秒)变化的规律如下表所示.下列这一变化过程中说法正确的是( )
A、 B、 C、 D、10. 有一种手持烟花,点然后每隔 1.4 秒发射一发花弹。要求每一发花弹爆炸时的高度要超过 15 米,否则视为不合格,在一次测试实验中,该烟花发射出的第一发花弹的飞行高度(米)随飞行时间(秒)变化的规律如下表所示.下列这一变化过程中说法正确的是( ) A、飞行时间 t每增加 0.5 秒,飞行高度 h 就增加 5.5 米 B、飞行时间 t 每增加 0.5 秒,飞行高度 h 就减少 5.5 米 C、估计飞行时间 t 为 5 秒时,飞行高度 h 为 11.8 米 D、只要飞行时间 t 超过 1.5 秒后该花弹爆炸,就视为合格
A、飞行时间 t每增加 0.5 秒,飞行高度 h 就增加 5.5 米 B、飞行时间 t 每增加 0.5 秒,飞行高度 h 就减少 5.5 米 C、估计飞行时间 t 为 5 秒时,飞行高度 h 为 11.8 米 D、只要飞行时间 t 超过 1.5 秒后该花弹爆炸,就视为合格二、填空题
-
11. 若 ,则 的值为 .12. 如图是一个可以只有转动的转盘,被等分成六个扇形,请在转盘适当的扇形区域内涂上阴影,使只自由转动的该转盘停止转动时,指针指向阴影区域的概率是 .
 13. 如图, 中, , 是 边上的中线, 的平分线交 于点 , 于点 ,若 ,则 的长度为 .
13. 如图, 中, , 是 边上的中线, 的平分线交 于点 , 于点 ,若 ,则 的长度为 . 14. 把长和宽分别为 和 的四个相同的小长方形拼成如图的图形,若图中每个小长方形的面积均为 ,大正方形的面积为 ,则 的值为 .
14. 把长和宽分别为 和 的四个相同的小长方形拼成如图的图形,若图中每个小长方形的面积均为 ,大正方形的面积为 ,则 的值为 . 15. 如图,已知 中,点 在 边上(点 与点 不重合),且 ,连接 ,沿 折叠 使点 落到点 处,得到 .若 ,则 的度数为 (用含 的式子表示).
15. 如图,已知 中,点 在 边上(点 与点 不重合),且 ,连接 ,沿 折叠 使点 落到点 处,得到 .若 ,则 的度数为 (用含 的式子表示).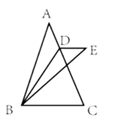 16. 计算:(1)、 ;(2)、 ;(3)、 ;(4)、 .17. 先化简,再求值; ,其中18. 某餐厅新开业,为了吸引顾客,推出“模球有礼”优惠活动,餐厅在一个不透明的纸箱中装入除颜色外完全相同的小球共 个,其中红色球 个、黄色球 个、蓝色球 个,剩余为绿色。用餐结束后,顾客在结账前有一次模奖机会,可以从纸箱中任意摸出一一球(记下颜色后放回),根据摸到的小球颜色决定这一次用餐可享受的优息(如下表所示).求某顾客通过摸球获得餐费打折优惠的概率。
16. 计算:(1)、 ;(2)、 ;(3)、 ;(4)、 .17. 先化简,再求值; ,其中18. 某餐厅新开业,为了吸引顾客,推出“模球有礼”优惠活动,餐厅在一个不透明的纸箱中装入除颜色外完全相同的小球共 个,其中红色球 个、黄色球 个、蓝色球 个,剩余为绿色。用餐结束后,顾客在结账前有一次模奖机会,可以从纸箱中任意摸出一一球(记下颜色后放回),根据摸到的小球颜色决定这一次用餐可享受的优息(如下表所示).求某顾客通过摸球获得餐费打折优惠的概率。 19. 已知:如图 ,点 是 延长线上的一点,且 ,求作: ,使 且点 与点 在同侧.(要求:尺规作图,保留作图痕迹)
19. 已知:如图 ,点 是 延长线上的一点,且 ,求作: ,使 且点 与点 在同侧.(要求:尺规作图,保留作图痕迹) 20. 如图,已知 和 的边 和 在同一直线上, ,点 在直线 的两侧, ,判断 与 的数量关系和位置关系,并说明理由.
20. 如图,已知 和 的边 和 在同一直线上, ,点 在直线 的两侧, ,判断 与 的数量关系和位置关系,并说明理由.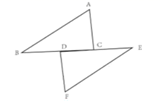 21. 在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的竟是关系:
21. 在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的竟是关系: (1)、在这个变化过程中,自变量是 , 因变量是;(2)、在当地温度 每增加 ,这种蟋蟀 叫的次数 是怎样变化的?(3)、这种蟋蟀 叫的次数 (次)与当地温度 之间的关系为;(4)、当这种蟋蟀 叫的次数 时,求当时该地的温度.22. 阅读下列材料,完成相应的任务;全等四边形根据全等图形的定又可知:四条边分别相等、四个角也分别相等的两个四边形全等。在“探索三角形全等的条件”时,我们把两个三角形中“一条边和等”或“一个角相等”称为一个条件.智慧小组的同学类比“探索三角形全等条件”的方法探索“四边形全等的条件”,进行了如下思考:如图1,四边形 和四边形 中,连接对角线 ,这样两个四边形全等的问题就转化为“ ”与“ ”的问题。若先给定“ ”的条件,只要再增加 个条件使“ ”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。
(1)、在这个变化过程中,自变量是 , 因变量是;(2)、在当地温度 每增加 ,这种蟋蟀 叫的次数 是怎样变化的?(3)、这种蟋蟀 叫的次数 (次)与当地温度 之间的关系为;(4)、当这种蟋蟀 叫的次数 时,求当时该地的温度.22. 阅读下列材料,完成相应的任务;全等四边形根据全等图形的定又可知:四条边分别相等、四个角也分别相等的两个四边形全等。在“探索三角形全等的条件”时,我们把两个三角形中“一条边和等”或“一个角相等”称为一个条件.智慧小组的同学类比“探索三角形全等条件”的方法探索“四边形全等的条件”,进行了如下思考:如图1,四边形 和四边形 中,连接对角线 ,这样两个四边形全等的问题就转化为“ ”与“ ”的问题。若先给定“ ”的条件,只要再增加 个条件使“ ”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。按照智慧小组的思路,小明对图 中的四边形 与四边形 先给出和下条件: , ,小亮在此基础上又给出“ ”两个条件.他们认为满足这五个条件能得到“四边形 四边形 ”.
 (1)、请根据小明和小亮给出的条件,说明“四边形 四边形 ”的理由;(2)、请从下面 两题中任选一题作答,我选择题.
(1)、请根据小明和小亮给出的条件,说明“四边形 四边形 ”的理由;(2)、请从下面 两题中任选一题作答,我选择题.在材料中“小明所给条件”的基础上,小颖又给出两个条件“ ”.满足这五个条件 (填“能”或“不能”)得到四边形 四边形
在材料中“小明所给条件的基础上”,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形 四边形 ,你添加的条件是① , ②.
23. 综合与探究数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.

初步探究:
(1)、在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由; (2)、小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
(2)、小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.请从下面 A,B 两题中任选一题作答,我选择题.
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.

B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
