山西省临汾市襄汾县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期：2020-06-08 类型：期末考试
一、选择题
-
1. 方程- x=3的解是（ ）A、x=-1 B、-6 C、- D、-92. 下列图形中，是轴对称图形但不是中心对称图形的是（ ）A、
B、
C、
D、
3. 若a＞b，则下列各式中正确的是（ ）A、a-c＜b-c B、ac＞bc C、- （c≠0） D、a（c2+1）＞b（c2+1）4. 下列方程的解法中，错误的个数是（ ）①方程2x-1=x+1移项，得3x=0②方程 =1去分母，得x-1=3=x=4③方程1- 去分母，得4-x-2=2（x-1）④方程 去分母，得2x-2+10-5x=1
A、1 B、2 C、3 D、45. 如图，直线AB∥EF，点C是直线AB上一点，点D是直线AB外一点，若∠BCD=100°，∠CDE=15°，则∠DEF的度数是（ ）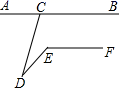
A、110° B、115° C、120° D、125°6. 已知 是二元一次方程组 的解，则2a+b的值为（ ）A、3 B、4 C、5 D、67. 已知等腰△ABC的周长为10，若设腰长为x，则x的取值范围是（ ）A、 ＜x＜5 B、0＜x＜2.5 C、0＜x＜5 D、0＜x＜108. 能够铺满地面的正多边形组合是（ ）A、正三角形和正五边形 B、正方形和正六边形 C、正方形和正五边形 D、正五边形和正十边形9. 若四边形ABCD中，∠A：∠B：∠C=1：2：5，且∠C=150°，则∠D的度数为（ ）A、90° B、105° C、120° D、135°10. 如图，将正方形纸片 折叠，使点 落在边 上的 处，点 落在 处，若 ，则 的度数为（ ）
A、100° B、110° C、120° D、130°二、填空题
-
11. 若一个正多边形的每一个外角都是30°，则这个正多边形的边数为 ．12. 我国古代数学名著《孙子算经》中有这样一题，今有鸡兔同笼，上有35头，下有94足，问鸡兔各几何？此题的答案是：鸡有23只，兔有12只，现在小敏将此题改编为：今有鸡兔同笼，上有33头，下有88足，问鸡兔各几何？则此时的答案是：鸡有只，兔有只．13. 如图，一副三角尺△ABC与△ADE的两条斜边在一条直线上，直尺的一边GF∥AC，则∠DFG的度数为.
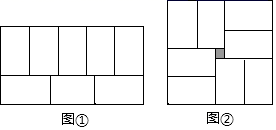
14. 若不等式组 的解集是x＞1，则m的取值范围是15. 如图是由四块长方形纸片和一块正方形纸片拼成一个大正方形．已知其中的两块，一块长为5cm，宽为2cm；一块长为4cm，宽为1cm，则大正方形的面积为cm2 ．
三、综合题
-
16. 解方程（组）：(1)、 ；(2)、 ．17. 解不等式组 并把它的解集表示在数轴上．18. 如图，在4×4的方格纸中，△ABC的三个顶点都在格点上．
(1)、在图1中，画出一个与△ABC成中心对称的格点三角形；(2)、在图2中，画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形；(3)、在图3中，画出△ABC绕着点C按顺时针方向旋转90°后的三角形；(4)、在图4中，画出所有格点△BCD，使△BCD为等腰直角三角形，且S△BCD=4．19. 用※定义一种新运算：对于任意有理数a和b，规定a※b=ab2+2ab+a，如1※2=1×22+2×1×2+1=9(1)、求（-4）※ 3；(2)、若 ※3=-16，求a的值．20. 如图，将△ABC绕点C顺时针旋转90°得到△EDC．若点A、D、E在同一条直线上，且∠ACB=20°，求∠CAE及∠B的度数．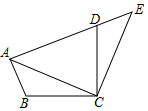
21. 某校计划组织师生共300人参加一次大型公益活动，如果租用6辆大客车和5辆小客车，恰好全部坐满，已知每辆大客车的乘客座位数比小客车多17个．(1)、求每辆大客车和每辆小客车的乘客座位数；(2)、由于最后参加活动的人数增加了30人，学校决定调整租车方案，在保持租用车辆总数不变的情况下，且所有参加活动的师生都有座位，求租用小客车数量的最大值．
