山西省晋中市灵石县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-06-08 类型:期末考试
一、选择题
-
1. 为丰富国民精神文化生活,提升文化素养,全国各地陆续开展全民阅读活动. 现在的图书馆不单是人们学习知识的地方,更是成为人们休闲的好去处. 下列图书馆标志的图形中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算中正确的是( )A、 B、 C、 D、3. 下列不是必然事件的是( )A、角平分线上的点到角两边距离相等 B、三角形两边之和大于第三边 C、三角形重心到三个顶点的距离不相等 D、面积相等的两三角形全等4. 已知 ,则 的大小关系是( )A、 B、 C、 D、5. 如图,等腰直角三角形的顶点A,C分别在直线a、b上,若a∥b,∠1=30°,则∠2的度数为( )
2. 下列运算中正确的是( )A、 B、 C、 D、3. 下列不是必然事件的是( )A、角平分线上的点到角两边距离相等 B、三角形两边之和大于第三边 C、三角形重心到三个顶点的距离不相等 D、面积相等的两三角形全等4. 已知 ,则 的大小关系是( )A、 B、 C、 D、5. 如图,等腰直角三角形的顶点A,C分别在直线a、b上,若a∥b,∠1=30°,则∠2的度数为( )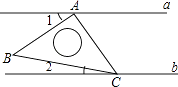 A、30° B、15° C、10° D、20°6. 已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )A、8或10 B、8 C、10 D、6或127. 如图, 是 的角平分线,点 在 上,且 于点 , , ,则 的度数为( )
A、30° B、15° C、10° D、20°6. 已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )A、8或10 B、8 C、10 D、6或127. 如图, 是 的角平分线,点 在 上,且 于点 , , ,则 的度数为( )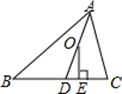 A、 B、 C、 D、8. 如图,直线l是一条河,A、B 是两个新农村定居点.欲在 l 上的某点处修建一个水泵站,由水泵站直接向 A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管 道最短的方案是( )
A、 B、 C、 D、8. 如图,直线l是一条河,A、B 是两个新农村定居点.欲在 l 上的某点处修建一个水泵站,由水泵站直接向 A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管 道最短的方案是( ) A、
A、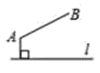 B、
B、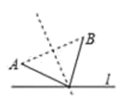 C、
C、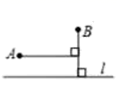 D、
D、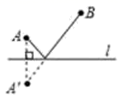 9. 如图中任意画一个点,落在黑色区域的概率是( )
9. 如图中任意画一个点,落在黑色区域的概率是( )
A、 B、 C、π D、5010. 如图,长方形 的边 ,沿 折叠,使点 落在点 处,点 落在点 处,若 ,则 ( )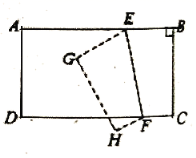 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若an=3,则a2n= .12.
如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: , 使△AEH≌△CEB.
 13. 等腰三角形一腰上的高与另一腰所夹角为40°,则该等腰三角形底角为14. 如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于 CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为 .
13. 等腰三角形一腰上的高与另一腰所夹角为40°,则该等腰三角形底角为14. 如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于 CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为 .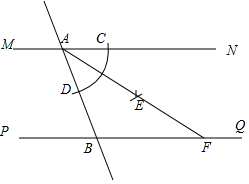 15. 已知 ,点 在 的内部, 与 关于 对称, 与 关于 对称, .16. 计算:(1)、(2)、(3)、已知 ,求 的值.17. 如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地,规划部门计划将阴影部分进行绿化,中间将修建一座边长为(a+b)米的正方形雕像.
15. 已知 ,点 在 的内部, 与 关于 对称, 与 关于 对称, .16. 计算:(1)、(2)、(3)、已知 ,求 的值.17. 如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地,规划部门计划将阴影部分进行绿化,中间将修建一座边长为(a+b)米的正方形雕像. (1)、试用含a、b的式子表示绿化部分的面积(结果要化简).(2)、若a=3,b=2,请求出绿化部分的面积.18. 请在网格中完成下列问题:
(1)、试用含a、b的式子表示绿化部分的面积(结果要化简).(2)、若a=3,b=2,请求出绿化部分的面积.18. 请在网格中完成下列问题: (1)、如图1,网格中的△ABC与△DEF为轴对称图形,请用所学轴对称的知识作出△ABC与△DEF的对称轴l;(2)、如图2,请在图中作出△ABC关于直线MN成轴对称的图形△A′B′C′.19. 某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
(1)、如图1,网格中的△ABC与△DEF为轴对称图形,请用所学轴对称的知识作出△ABC与△DEF的对称轴l;(2)、如图2,请在图中作出△ABC关于直线MN成轴对称的图形△A′B′C′.19. 某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题: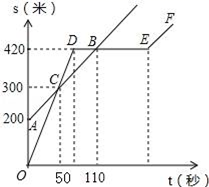 (1)、在上述变化过程中,自变量是 , 因变量是;(2)、朱老师的速度为米/秒;小明的速度为米/秒;(3)、小明与朱老师相遇次,相遇时距起点的距离分别为米.20. 某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,由以上信息能求出CB的长度吗?请你说明理由.
(1)、在上述变化过程中,自变量是 , 因变量是;(2)、朱老师的速度为米/秒;小明的速度为米/秒;(3)、小明与朱老师相遇次,相遇时距起点的距离分别为米.20. 某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,由以上信息能求出CB的长度吗?请你说明理由.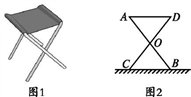 21. 在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).
21. 在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).

⑴一个不透明的盒子里装有4个红球,2个白球,除颜色外其它都相同,搅均后,从中随意摸出一个球,摸出红球的可能性是多少?解:P(摸出一个红球)= .
⑵口袋里装有如图所示的1角硬币2枚、5角硬币2枚、1 元硬币1枚.搅均后,从中随意摸出一枚硬币,摸出1角硬币的可能性是多少?解:P(摸出1角的硬币)= .
⑶如图,是一个转盘,盘面上有5个全等的扇形区域,每个区域显示有不同的颜色,轻轻转动转盘,当转盘停止后,指针对准红色区域的可能性是多少?解:P(指针对准红色区域)= .
问题:根据以上材料回答问题:小敏,小聪,小丽三人中,谁编写的试题及解答是正确的,并简要说明其他两人所编试题或解答的不足之处.
22. 综合与实践:(1)、如图,已知:在等腰直角 中, , ,直线 经过点 , 直线 , 直线 ,垂足分别为点 、 .小明观察图形特征后猜想线段 、 和 之间存在 的数量关系,请你判断他的猜想是否正确,并说明理由. (2)、如图,将(1)中的条件改为: 为等边三角形, 、 、 三点都在直线 上,并且有 ,请问结论 是否成立?并说明理由.
(2)、如图,将(1)中的条件改为: 为等边三角形, 、 、 三点都在直线 上,并且有 ,请问结论 是否成立?并说明理由.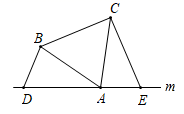 (3)、如图,若将(1)中的三角形变形为一般的等腰三角形, 中, , ,其中 为任意锐角或钝角, 、 、 三点都在直线 上.问:满足什么条件时,结论 仍成立?直接写出条件即可.
(3)、如图,若将(1)中的三角形变形为一般的等腰三角形, 中, , ,其中 为任意锐角或钝角, 、 、 三点都在直线 上.问:满足什么条件时,结论 仍成立?直接写出条件即可.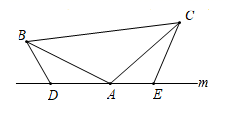 23. 直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B 在射线OM上运动.
23. 直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B 在射线OM上运动.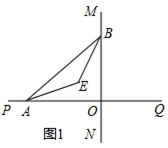
 (1)、如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,直接写出∠AEB的大小;(2)、如图2,已知AC、BC分别是∠BAP和∠ABM角的平分线,点A、B在运动的过程中,∠ACB的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的大小;
(1)、如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,直接写出∠AEB的大小;(2)、如图2,已知AC、BC分别是∠BAP和∠ABM角的平分线,点A、B在运动的过程中,∠ACB的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的大小;