山西省大同市2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-06-08 类型：期末考试

进入出卷网下载

一、选择题

1. 已知实数a，b满足a+1＞b+1，则下列选项错误的为（）

A、a＞b B、a+2＞b+2 C、﹣a＜﹣b D、2a＞3b

查看试题解析
2. 如图，图中∠1与∠2是内错角的是（）

A、a和b B、b和c C、c和d D、b和d

查看试题解析
3. 关于 $\sqrt{12}$ 的叙述，错误的是（）

A、 $\sqrt{12}$ 是有理数 B、面积为12的正方形的边长是 $\sqrt{12}$ C、 $\sqrt{12}$ ＝2 $\sqrt{3}$ D、在数轴上可以找到表示 $\sqrt{12}$ 的点

查看试题解析
4. 方程组 ${\begin{array}{l} x + y = 6 \\ x - 3 y = - 2 \end{array}$ 的解是（）．

A、 ${\begin{array}{l} x = 5 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = - 4 \\ y = - 2 \end{array}$ C、 ${\begin{array}{l} x = - 5 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = 4 \\ y = 2 \end{array}$

查看试题解析
5. 在平面直角坐标系中，点P（m-3，4-2m）不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 下面调查方式中，合适的是（）

A、调查你所在班级同学的身高，采用抽样调查方式 B、调查大汶河的水质情况，采用抽样调查的方式 C、调查CCTV-5《NBA 总决赛》栏目在我市的收视率，采用普查的方式 D、要了解全市初中学生的业余爱好，采用普查的方式

查看试题解析
7. 如图所示，数轴上表示2， $\sqrt{5}$ 的对应点分别为C，B，点C是AB的中点，则点A表示的数是（）

A、 $1$ B、 $2 - \sqrt{5}$ C、 $4 - \sqrt{5}$ D、 $\sqrt{5} - 2$

查看试题解析
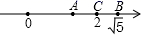8. 下列哪个选项中的不等式与不等式 $5 x > 8 + 2 x$ 组成的不等式组的解集为 $\frac{8}{3} < x < 5$ .（）

A、 $x + 5 < 0$ B、 $2 x > 10$ C、 $3 x - 15 < 0$ D、 $- x - 5 > 0$

查看试题解析
9. 某商场为了解本商场的服务质量，随机调查了本商场的100名顾客，调查的结果如图所示．根据图中给出的信息，这100名顾客中对该商场的服务质量表示不满意的有（）

A、46人 B、38人 C、9人 D、7人

查看试题解析
10. 定义：直线l₁与l₂相交于点O，对于平面内任意一点M，点M到直线l₁、l₂的距离分别为p、q，则称有序实数对（p，q）是点M的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. $\sqrt{16}$ 的算术平方根是， $\sqrt{5}$ ﹣2的相反数是　， $\sqrt[3]{- 8}$ 的绝对值是．

查看试题解析
12. 如图，如果将面积为5的△ABC沿BC方向平移至△DEF的位置，平移的距离是边BC长的两倍，那么图中四边形ACED的面积为.

查看试题解析
13.
在大课间活动中，同学们积极参加体育锻炼，小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试，并以测试数据为样本绘制如图所示的部分频数分布直方图（从左到右依次分为六个小组，每小组含最小值，不含最大值）和扇形统计图，若“一分钟跳绳”次数不低于130次的成绩为优秀，全校共有1200名学生，根据图中提供的信息，估计该校学生“一分钟跳绳”成绩优秀的人数为人．

查看试题解析
14. 小强同学生日的月数减去日数为2，月数的两倍和日数相加为31，则小强同学生日的月数和日数的和为

查看试题解析
15. 已知a，b是正整数，若 $\frac{\sqrt{7}}{a} + \frac{\sqrt{10}}{b}$ 是不大于2的整数，则满足条件的有序数对（a，b）为

查看试题解析
16. 解下列不等式组，并将它的解集在数轴上表示出来．
${\begin{array}{l} x - 1 > 2 x \\ \frac{x - 1}{3} \leq \frac{x + 1}{9} \end{array}$ ．

查看试题解析

三、综合题

17. 解方程组： ${\begin{array}{l} x - 2 y ＝ 2 \\ 2 x + 4 y ＝ 12 \end{array}$

查看试题解析
18. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为（﹣4，5），（﹣1，3）．

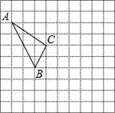(1)、请在如图所示的网格平面内作出平面直角坐标系；

(2)、请把△ABC先向右移动5个单位，再向下移动3个单位得到△A′B′C′，在图中画出△A′B′C′；

(3)、求△ABC的面积．

查看试题解析

19. 某地某月1～20日中午12时的气温（单位：℃）如下：

22 31 25 15 18 23 21 20 27 17 20 12 18 21 21 16 20 24 26 19

(1)、将下列频数分布表补充完整：

气温分组	划记	频数
12≤x＜17		3
17≤x＜22		10
22≤x＜27		5
27≤x＜32		2

(2)、补全频数分布直方图；

(3)、根据频数分布表或频数分布直方图，分析数据的分布情况．

查看试题解析

20. 食品安全是老百姓关注的话题，在食品中添加过量的添加剂对人体有害，但适量的添加剂对人体无害且有利于食品的储存和运输．某饮料加工厂生产的A、B两种饮料均需加入同种添加剂，A饮料每瓶需加该添加剂0.2克，B饮料每瓶需加该添加剂0.3克，已知54克该添加剂恰好生产了A、B两种饮料共200瓶，问A、B两种饮料各生产了多少瓶？

查看试题解析
21. 某公交公司有A，B型两种客车，它们的载客量和租金如下表：

A

B

载客量（人/辆）

45

30

租金（元/辆）

400

280

某中学根据实际情况，计划租用A，B型客车共5辆，同时送七年级师生到基地校参加社会实践活动．设租用A型客车x辆，根据要求回答下列问题：

(1)、用含x的式子填写下表：

车辆数（辆）

载客量

租金（元）

A

x

45x

400x

B

5-x

(2)、若要保证租车费用不超过1900元，求x的最大值．

查看试题解析
22. 如图，点D为射线CB上一点，且不与点B、C重合，DE∥AB交直线AC于点E，DF∥AC交直线AB于点F.画出正确的图形，猜想∠EDF与∠BAC的数量关系，并说明理由.

查看试题解析
23. 如图，已知AM∥BN，∠A=60°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．

(1)、求∠CBD的度数；

(2)、当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．

(3)、当点P运动到使∠ACB=∠ABD时，直接写出∠ABC的度数．

查看试题解析

	A	B
载客量（人/辆）	45	30
租金（元/辆）	400	280

	车辆数（辆）	载客量	租金（元）
A	x	45x	400x
B	5-x