浙江省杭州市西湖区2020年数学中考模拟试卷（4月）

试卷更新日期：2020-06-05 类型：中考模拟

进入出卷网下载

一、选择题（本大题有10小题，每小题3分，共30分。）

1. 下列实数中，无理数是（）

A、π B、﹣ $\frac{7}{2}$ C、 $\sqrt{25}$ D、|﹣4|

查看试题解析
2. 若点P（2，﹣3）与点Q（x，y）关于x轴对称，则x，y的值分别是（）

A、﹣2，3 B、2，3 C、﹣2，﹣3 D、2，﹣3

查看试题解析
3. 如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据求得这个几何体的侧面积是（）

A、12cm² B、（12+π）cm² C、6πcm² D、8πcm²

查看试题解析
4. 如图，已知点A，B，C，D，E是⊙O的五等分点，则∠BAD的度数是（）

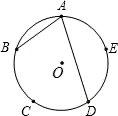A、36° B、48° C、72° D、96°

查看试题解析
5. 下列4个图案中，轴对称图形的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

6. 为了更好地迎接庐阳区排球比赛，某校积极准备，从全校学生中遴选出21名同学进行相应的排球训练，该训练队成员的身高如下表：

身高（cm）	170	172	175	178	180	182	185
人数（个）	2	4	5	2	4	3	1

则该校排球队21名同学身高的众数和中位数分别是（单位：cm）（　　）

A、185，178 B、178，175 C、175，178 D、175，175

查看试题解析

7. 如图，在△ABC中，∠B＝50°，∠C＝30°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点M，N，作直线MN交BC于点D，连接AD，则∠BAD的度数为（）

A、50° B、60° C、70° D、80°

查看试题解析
8. 三角形的两边长分别为3和6，第三边的长是方程x²﹣6x+8=0的一个根，则这个三角形的周长是（　　）

A、9 B、11 C、13 D、14

查看试题解析
9. 某山区有一种土特产品，若加工后出售，单价可提高20%，但重量会减少10%.现有该种土特产品300千克，全部加工后可以比不加工多卖240元，设加工前单价是x元/kg，加工后的单价是y元/kg，由题意，可列出关于x，y的方程组是（）

A、 ${\begin{matrix} y = (1 - 20 %) x \\ 300 (1 - 10 %) y - 300 x = 240 \end{matrix}$ B、 ${\begin{matrix} y = (1 - 20 %) x \\ 300 (1 + 10 %) y - 300 x = 240 \end{matrix}$ C、 ${\begin{matrix} y = (1 + 20 %) x \\ 300 (1 + 10 %) y - 300 x = 240 \end{matrix}$ D、 ${\begin{matrix} y = (1 + 20 %) x \\ 300 (1 - 10 %) y - 300 x = 240 \end{matrix}$

查看试题解析
10. 如图，一次函数与反比例函数的图象交于A（1，8）和B（4，2）两点，点P是线段AB上一动点（不与点A和B重合），过P点分别作x轴，y轴的垂线PC，PD交反比例函数图象于点E，F，则四边形OEPF面积的最大值是（）

A、3 B、4 C、 $\frac{9}{2}$ D、6

查看试题解析

二、填空题（本大题有6小题，每小题4分，共24分）

11. 分解因式：2x²+x﹣6＝.

查看试题解析
12. 2019年央视春晚创下了跨媒体收视传播新纪录.据统计，除夕当晚，海内外收视的观众总规模达11.73亿人.数据11.73亿人用科学记数法表示为人.

查看试题解析
13. 在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机地摸出一个小球不放回，再随机地摸出一个小球，则两次摸出的小球的标号的和为奇数的概率是.

查看试题解析
14. 若甲、乙两名同学五次数学模拟考试成绩的平均分都是135分，且甲同学成绩的方差S_甲²＝1.05，乙同学成绩的方差S_乙²＝0.41，则甲、乙两名同学成绩相对稳定的是.

查看试题解析
15. 在△ABC中，AB＝AC＝2，BD是AC边上的高，且BD＝ $\sqrt{3}$ ，则∠ACB的度数是.

查看试题解析
16. 如图，直角三角形纸片的两直角边长分别为4，8，现将△ABC如图那样折叠，使点A与点B重合，折痕为DE，则tan∠CBE的值是.

查看试题解析

三、解答题（本大题有7个小题，共66分）

17. 先化简，再求代数式 $(\frac{1}{a + 1} - \frac{a - 2}{a^{2} - 1}) \div \frac{1}{a + 1}$ 的值，其中 $a = 2 sin 60 ° + tan 45 °$ .

查看试题解析
18. 如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F.

(1)、求证：四边形BEDF为菱形；

(2)、如果∠A＝90°，∠C＝30°，BD＝12，求菱形BEDF的面积.

查看试题解析
19. 网络时代，新兴词汇层出不穷.为了解大众对网络词汇的理解，某兴趣小组举行了一个“我是路人甲”的调查活动：选取四个热词A：“硬核人生”，B：“好嗨哦”，C：“双击666”，D：“杠精时代”在街道上对流动人群进行了抽样调查，要求被调查的每位只能勾选一个最熟悉的热词，根据调查结果，该小组绘制了如下的两幅不完整的统计图，请你根据统计图提供的信息，解答下列问题：

(1)、本次调查中，一共调查了名路人.

(2)、补全条形统计图；

(3)、扇形图中的b＝.

查看试题解析
20. 如图，在Rt△ABC中，∠C＝90°，∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O，使⊙O经过点A和点D.

(1)、判断直线BC与⊙O的位置关系，并说明理由；

(2)、若AC＝3，∠B＝30°.
①求⊙O的半径；

②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.（结果保留根号和π）

查看试题解析
21. 如图1，△ABC是边长为4cm的等边三角形，边AB在射线OM上，且OA＝6cm，点D从O点出发，沿OM的方向以1cm/s的速度运动，当D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连结DE.

(1)、求证：△CDE是等边三角形；

(2)、如图2，当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE的最小周长；若不存在，请说明理由；

(3)、如图3，当点D在射线OM上运动时，是否存在以D、E、B为顶点的三角形是直角三角形？若存在，求出此时t的值；若不存在，请说明理由.

查看试题解析
22. 某旅行团32人在景区A游玩，他们由成人、少年和儿童组成．已知儿童10人，成人比少年多12人．

(1)、求该旅行团中成人与少年分别是多少人?

(2)、因时间充裕，该团准备让成人和少年（至少各1名）带领10名儿童去另一景区B游玩．景区B的门票价格为100元/张，成人全票，少年8折，儿童6折，一名成人可以免费携带一名儿童．①若由成人8人和少年5人带队，则所需门票的总费用是多少元?②若剩余经费只有1200元可用于购票，在不超额的前提下，最多可以安排成人和少年共多少人带队?求所有满足条件的方案，并指出哪种方案购票费用最少．

查看试题解析
23. 如图，已知抛物线y＝ax²+bx+c（a≠0）的对称轴为直线x＝﹣1，且抛物线经过点A（1，0），C（0，3）两点，与x轴交于点B.

(1)、若直线y＝mx+n经过B，C两点，求直线BC和抛物线的表达式；

(2)、在抛物线的对称轴x＝﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；

(3)、设点P为抛物线的对称轴x＝﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标.

查看试题解析