浙江省舟山市2020年数学中考仿真模拟试卷
试卷更新日期:2020-06-05 类型:中考模拟
一、选择题(本题有10小题,每题3分,共30分。)
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 截止到2019年9月3日,电影《哪吒之魔童降世》的累计票房达到了47.24亿,47.24亿用科学记数法表示为( )A、47.24×109 B、4.724×109 C、4.724×105 D、472.4×1053. 下列立体图形中,主视图是三角形的是( )。A、
 B、
B、 C、
C、 D、
D、 4. 某商店根据今年6﹣10月份的销售额情况,制作了如下统计图.根据图中信息,可以判断相邻两个月销售额变化最大的是( )
4. 某商店根据今年6﹣10月份的销售额情况,制作了如下统计图.根据图中信息,可以判断相邻两个月销售额变化最大的是( ) A、6月到7月 B、7月到8月 C、8月到9月 D、9月到10月5. 不等式4+2x>0的解集在数轴上表示为( )A、
A、6月到7月 B、7月到8月 C、8月到9月 D、9月到10月5. 不等式4+2x>0的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 6. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
6. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )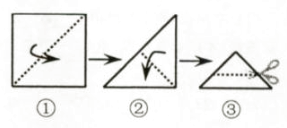 A、
A、 B、
B、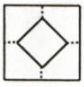 C、
C、 D、
D、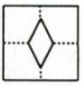 7. 下列不等式的变形不正确的是( )A、若a>b,则a+3>b+3 B、若﹣a>﹣b,则a<b C、若﹣ x<y,则x>﹣2y D、若﹣2x>a,则x>﹣ a8. 足球比赛中,每场比赛都要分出胜负每队胜1场得3分,负一场扣1分,某队在8场比赛中得到12分,若设该队胜的场数为x负的场数为y,则可列方程组为( )A、 B、 C、 D、9. 第一次:将点A绕原点O逆时针旋转90°得到A1;
7. 下列不等式的变形不正确的是( )A、若a>b,则a+3>b+3 B、若﹣a>﹣b,则a<b C、若﹣ x<y,则x>﹣2y D、若﹣2x>a,则x>﹣ a8. 足球比赛中,每场比赛都要分出胜负每队胜1场得3分,负一场扣1分,某队在8场比赛中得到12分,若设该队胜的场数为x负的场数为y,则可列方程组为( )A、 B、 C、 D、9. 第一次:将点A绕原点O逆时针旋转90°得到A1;第二次:作点A1关于x轴的对称点A2;
第三次:将点A2绕点O逆时针旋转90°得到A3;
第四次:作点A3关于x轴的对称点A4…,
按照这样的规律,点A35的坐标是( )
 A、(﹣3,2) B、(﹣2,3) C、(﹣2.﹣3) D、(3.﹣2)10. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,点B位于(4,0)、(5,0)之间,与y轴交于点C,对称轴为直线x=2,直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴上方且横坐标小于5,则下列结论:①4a+b+c>0;②a﹣b+c<0;③m(am+b)<4a+2b(其中m为任意实数);④a<﹣1,其中正确的是( )
A、(﹣3,2) B、(﹣2,3) C、(﹣2.﹣3) D、(3.﹣2)10. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,点B位于(4,0)、(5,0)之间,与y轴交于点C,对称轴为直线x=2,直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴上方且横坐标小于5,则下列结论:①4a+b+c>0;②a﹣b+c<0;③m(am+b)<4a+2b(其中m为任意实数);④a<﹣1,其中正确的是( ) A、①②③④ B、①②③ C、①②④ D、①③④
A、①②③④ B、①②③ C、①②④ D、①③④二、填空题(共6小题,每小题4分,满分24分)
-
11. 因式分解:x﹣x2= .12. 如图,a∥b∥c,BC=1,DE=4.5,EF=1.5,则AC=.
 13. 小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是 , 据此判断该游戏(填“公平”或“不公平”).14. 若关于x的一元二次方程x2+x+k=0有两个不相等的实数根,则k的取值范围是.15. 如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D,若AB=4,AC=3,则cos∠BAD的值为.
13. 小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是 , 据此判断该游戏(填“公平”或“不公平”).14. 若关于x的一元二次方程x2+x+k=0有两个不相等的实数根,则k的取值范围是.15. 如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D,若AB=4,AC=3,则cos∠BAD的值为. 16. 如图,等腰直角△ABC中,∠ACB=90°,AC=BC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,则点D在运动过程中ME的最小值为.
16. 如图,等腰直角△ABC中,∠ACB=90°,AC=BC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,则点D在运动过程中ME的最小值为.
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17.(1)、计算:( )2﹣2﹣1×(﹣4);(2)、化简:(m+2)(m﹣2)﹣ ×3m.18. 小英解不等式 的过程如下,请指出她解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母得:3(1+x)﹣2(2x+1)≤1①去括号得:3+3x﹣4x+1≤1②
移项得:3x﹣4x≤1﹣3﹣1③合并同类项得:﹣x≤﹣3④
两边都除以﹣1得:x≤3⑤
19. 如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形. 20. 某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,过程如下,请补充完整.
20. 某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,过程如下,请补充完整.收集数据
从八、九两个年级各随机抽取20名学生,进行了体质健康测试,测试成绩(百分制)如下:
八年级
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
九年级
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据
按如下分数段整理、描述 这两组样本数据:
成绩
人数x
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
八年级
0
0
1
11
1
九年级
1
0
0
7
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示:
年级
平均数
中位数
众数
方差
八年级
78.3
77.5
75
33.6
九年级
78
80.5
52.1
(1)、请将以上两个表格补充完整;(2)、得出结论
估计九年级体质健康优秀的学生人数为;(3)、可以推断出年级学生的体质健康情况更好一些,理由为.(至少从两个不同的角度说明推断的合理性).21. 疫情突发,危难时刻,从决定建造到交付使用,雷神山、火神山医院仅用时十天,其建造速度之快,充分展现了中国基建的巨大威力!这样的速度和动员能力就是全国人民的坚定信心和尽快控制疫情的底气!改革开放40年来,中国已经成为领先世界的基建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点F在线段HG上运动,BC∥HG,AE⊥BC,垂足为点E,AE的延长线交HG于点G,经测量∠ABD=11°,∠ADE=26°,∠ACE=31°,BC=20m,EG=0.6m. (1)、求线段AG的长度;(结果精确到0.1m)(2)、连接AF,当线段AF⊥AC时,求点F和点G之间的距离.(结果精确到0.1m,参考数据:tan11°≈0.19,tan26°≈0.49,tan31°≈0.60)22. 已知在梯形ABCD中,AD∥BC , AC=BC=10,cos∠ACB= ,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB , DE的延长线与射线CB交于点F , 设AD的长为x .
(1)、求线段AG的长度;(结果精确到0.1m)(2)、连接AF,当线段AF⊥AC时,求点F和点G之间的距离.(结果精确到0.1m,参考数据:tan11°≈0.19,tan26°≈0.49,tan31°≈0.60)22. 已知在梯形ABCD中,AD∥BC , AC=BC=10,cos∠ACB= ,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB , DE的延长线与射线CB交于点F , 设AD的长为x .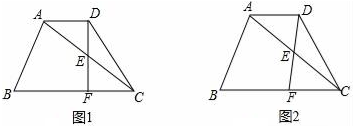 (1)、如图1,当DF⊥BC时,求AD的长;(2)、设EC=y , 求y关于x的函数解析式,并直接写出定义域;(3)、当△DFC是等腰三角形时,求AD的长.23. 如图,一次函数y=k1x+b(k1≠0)与反比例函数y= (k2≠0)的图象交于点A(﹣1,2),B(m,﹣1).
(1)、如图1,当DF⊥BC时,求AD的长;(2)、设EC=y , 求y关于x的函数解析式,并直接写出定义域;(3)、当△DFC是等腰三角形时,求AD的长.23. 如图,一次函数y=k1x+b(k1≠0)与反比例函数y= (k2≠0)的图象交于点A(﹣1,2),B(m,﹣1).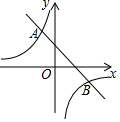 (1)、求这两个函数的表达式;(2)、在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.24. 如图①,在矩形ABCD中,已知BC=8cm,点G为BC边上一点,满足BG=AB=6cm,动点E以1cm/s的速度沿线段BG从点B移动到点G,连接AE,作EF⊥AE,交线段CD于点F.设点E移动的时间为t(s),CF的长度为y(cm),y与t的函数关系如图②所示.
(1)、求这两个函数的表达式;(2)、在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.24. 如图①,在矩形ABCD中,已知BC=8cm,点G为BC边上一点,满足BG=AB=6cm,动点E以1cm/s的速度沿线段BG从点B移动到点G,连接AE,作EF⊥AE,交线段CD于点F.设点E移动的时间为t(s),CF的长度为y(cm),y与t的函数关系如图②所示. (1)、图①中,CG=cm,图②中,m=;(2)、点F能否为线段CD的中点?若可能,求出此时t的值,若不可能,请说明理由;(3)、在图①中,连接AF,AG,设AG与EF交于点H,若AG平分△AEF的面积,求此时t的值.
(1)、图①中,CG=cm,图②中,m=;(2)、点F能否为线段CD的中点?若可能,求出此时t的值,若不可能,请说明理由;(3)、在图①中,连接AF,AG,设AG与EF交于点H,若AG平分△AEF的面积,求此时t的值.