浙江省台州市椒江区2020年初中毕业升学考试数学模拟试卷

试卷更新日期：2020-06-05 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分．）

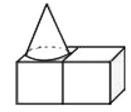
1. 单项式4ab²的系数为（）

A、1 B、2 C、3 D、4

查看试题解析
2. 如图是由两个小正方体和一个圆锥组成的立体图形，其主视图是（）

A、 B、 C、 D、

查看试题解析
3. 据台州市统计局调查数据显示，截至2019年年底，全市汽车保有量达到了1752000辆．将1752000用科学记数法表示是（）

A、0.1752×10⁶ B、0.1752×10⁷ C、1.752×10⁶ D、1.752×10⁷

查看试题解析
4. 一组数据5，4，3，6，6的中位数是（）

A、3 B、4 C、5 D、6

查看试题解析
5. 下列运算正确的是（）

A、 $a^{3} + a^{3} = a^{6}$ B、 ${(a^{3})}^{3} = a^{9}$ C、 $a^{3} \cdot a^{3} = a^{9}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
6. 如图，数轴上点A表示的数可能是下列各数中的（）

A、 $- \sqrt{11}$ B、 $-2 \sqrt{2}$ C、 $\sqrt[3]{- 26}$ D、 $- \sqrt{17}$

查看试题解析
7. 如图，四边形ABCD是半圆的内接四边形，AB是直径， = ．若∠C＝110°，则∠ABC的度数等于（）

A、55° B、60° C、65° D、70°

查看试题解析
8. 为抗击新型冠状肺炎，加强防疫措施，某口罩生产公司复工后每天的生产效率比原来提高了60%，结果提前15天完成了原计划200万只口罩的生产任务．设原计划x天完成任务，则下列方程正确的是（）

A、 $\frac{200}{x} - \frac{200}{(1 + 60 %) x} = 15$ B、 $\frac{200}{(1 + 60 %) x} - \frac{200}{x} = 15$ C、 $\frac{200}{x} = \frac{200}{x - 15} \times (1 + 60 %)$ D、 $\frac{200}{x} \times (1 + 60 %) = \frac{200}{x - 15}$

查看试题解析
9. 如图，在平面直角坐标系中，点A（1，2），在x轴上任取一点B，过点B作x轴的垂线BC．分别以A，B为圆心，大于 $\frac{1}{2}$ AB长为半径画弧，两弧相交于点D，E，连接DE，直线BC，DE相交于点P．设点P（x，y），则y关于x的函数关系用图象表示为（）

A、 B、 C、 D、

查看试题解析
10. 如图，四边形ABCD是正方形，G是BC上的任意一点，DE⊥AG于点E，BF∥DE且交AG于点F，若AB=3EF，则 $S_{阴影} ： S_{正方形 A B C D}$ 的值为（）

A、9： 16 B、2：3 C、4： 9 D、5：9

查看试题解析

二、填空题（本题有6小题，每小题5分，共30分)

11. $\sqrt{4}$ = ．

查看试题解析
12. 若 ${\begin{cases} x = 1 \\ y = - 2 \end{cases}$ 是关于x、y的二元一次方程ax+y＝3的解，则a＝．

查看试题解析
13. 一次函数y=（m﹣1）x+1，若y随x的增大而增大，则m的取值范围是．

查看试题解析
14. 从四张分别写着“中”“考”“加”“油”的卡片（大小、形状完全相同）中随机抽取两张，恰好是 “加”“油”两字的概率是．

查看试题解析
15. 在平面直角坐标系中，点P（2，m）绕坐标原点O逆时针旋转 $90 °$ 后，恰好落在图中阴影区域（包括边界）内，则m的取值范围是．

查看试题解析
16. 如图，在平行四边形ABCD中，AC⊥AB，AB=2，AC= $2 \sqrt{3}$ ．P、Q分别为边AD、DC上的动点，D₁是点D关于PQ的对称点，过点D₁作D₁F∥BC分别交AC、AB于点E、F，且满足D₁E：D₁F=1：3，则D₁F的最大值为．

查看试题解析

三、解答题（本题有8小题，第17 20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分

17. 计算： $| - 2 | - {(\frac{1}{2})}^{- 1} + 2 \cos 60 °$ ．

查看试题解析
18. 先化简，再求值： $(1 - \frac{1}{a}) \div \frac{a^{2} - 1}{a}$ ，其中a=2020．

查看试题解析
19. 随着车流量的增多，为了保障安全，方便行人过马路，近两年椒江区陆续建造了几座过街天桥. 区政府计划再建造一座至少高5米的过街天桥，现设计的天桥斜面倾斜角为32°，斜坡AB的长为10米，如图（1）所示，图（2）是其截面示意图．请问这样的设计是否符合要求？请说明理由．
（参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62．）

查看试题解析
20. 五一黄金周，小张一家自驾去某景点旅行．已知汽车油箱的容积为50 L，小张爸爸把油箱加满油后到了离加油站200 km的某景点，第二天沿原路返回．

(1)、油箱加满油后，求汽车行驶的总路程s（单位：km）与平均耗油量b(单位L/km)的函数关系式；

(2)、小张爸爸以平均每千米耗油0.1 L的速度驾驶到达目的地，返程时由于下雨，降低了车速，此时平均每千米的耗油量增加了一倍．如果小张爸爸始终以此速度行驶，不需要加油能否返回原加油站？如果不能，至少还需加多少油？

查看试题解析

21. 某中学为了解学生每周在校体育锻炼时间，在本校随机抽取了40名学生进行调查，并依据调查结果绘制了以下不完整的统计图表，请根据图表信息解答下列问题：

时间（小时）	频数（人数）	频率
2≤t＜3	4	0.1
3≤t＜4	10	0.25
4≤t＜5	a	0.15
5≤t＜6	8	b
6≤t＜7	12	0.3
合计	40	1

(1)、表中的a= ， b=；

(2)、请将频数分布直方图补全；

(3)、求这40名学生每周在校参加体育锻炼的平均时间；

(4)、若该校共有2400名学生，试估计全校每周在校参加体育锻炼时间至少有5小时的学生约为多少名？

查看试题解析

22. 如图（1），正五边形ABCDE与⊙O相切于点A，点C在⊙O上．

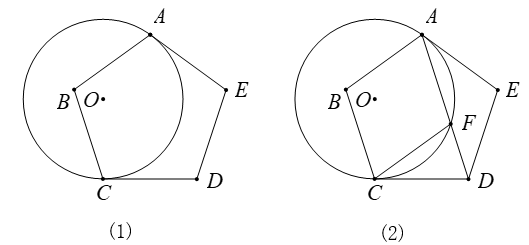(1)、求证：CD是⊙O的切线；

(2)、若⊙O的半径为5，求劣弧AC的长度；

(3)、如图（2），连接AD交⊙O于点F．求证：四边形ABCF是菱形．

查看试题解析
23. 已知抛物线 $y = x^{2} - b x + c$ （b，c为常数）与直线y=x-1交于x轴上同一点．

(1)、求b，c满足的关系式；

(2)、将此抛物线沿y轴翻折后得到的图象和原抛物线组成的新图象记为G．若直线y=3与图象G有且只有三个公共点，将直线y=3下方的部分（包括端点）记为图象W，求图象W表示的函数解析式；

(3)、在（2）的条件下，若点 $P (\frac{1}{2} ， m)$ ， $Q (x ， n) (- 4 \leq x < \frac{1}{2})$ 在图象W上．
① 试比较m，n的大小；

② 请直接写出 $\frac{m}{n}$ 的取值范围．

查看试题解析
24. 如图，在四边形ADBC中，BA平分∠DBC，且∠BDA=∠BAC= 90°，点E是BC的中
点，连接DE交AB于点F．

(1)、求证： $A B^{2} = B D \cdot B C$ ；

(2)、当∠DBA= 30°时，求 $\frac{B F}{B A}$ ；

(3)、是否存在点F，使F是AB的三等分点？若存在，请求出∠DBA的度数；若不存
在，请说明理由；

(4)、求∠BDE的最大值．

查看试题解析