江苏省宜兴市和桥联盟2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期：2020-06-05 类型：期中考试
一、选择题
-
1. 下列图案是一些汽车的车标，可以看作由“基本图案”平移得到的是（ ）A、
B、
C、
D、
2. 下列运算正确的是（ ）A、a2⋅a3=a6 B、a5+a3=a8 C、（a4）2=a6 D、a5÷a5=1（a≠0）3. 下列各式从左到右的变形，是因式分解的是（ ）A、x2-9+6x=（x+3）（x-3）+6x B、（x+5）（x-2）=x2+3x-10 C、x2-8x+16=（x-4）2 D、x2＋1＝x（x＋ ）4. 下列各式中，不能用平方差公式计算的是（ ）A、（﹣x﹣y）（x﹣y） B、（﹣x+y）（﹣x﹣y） C、（x+y）（﹣x+y） D、（x﹣y）（﹣x+y）5. 若 是一个完全平方式，则m的值是（ ）A、10 B、—10 C、-6或10 D、10或—106. 若M＝（x－3）（x－4），N＝（x－1）（x－6），则M与N的大小关系为（ ）A、M＞N B、M＝N C、M＜N D、由x的取值而定7. 已知三角形的两边分别为4和10，则此三角形的第三边可能是（ ）A、4 B、5 C、9 D、148. 一个正多边形每个外角都是30°，则这个多边形边数为（ ）
A、10 B、11 C、12 D、139. 如图，要得到AB∥CD，只需要添加一个条件，这个条件不可以是（ ）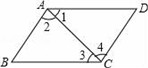
A、∠1＝∠3 B、∠B＋∠BCD＝180° C、∠2＝∠4 D、∠D＋∠BAD＝180°10. 如图，在△ABC中，点D，E分别在边BC，AC上，∠DCE＝∠DEC，点F在AC，点G在DE的延长线上，∠DFG＝∠DGF.若∠EFG＝35°，则∠CDF的度数为 （ ）
A、70° B、73° C、75° D、80°二、、填空题
-
11. 新型冠状病毒的直径约为0.0000001m，用科学记数法表示为m.12. 等腰三角形的两边长分别为 和 ，则它的周长是.13. 若（x+a）（x﹣2）的结果中不含关于字母x的一次项，则a=.
14. 边长为a、b的长方形的周长为16，面积为10，则a2b+ab2=.15. 如图，一把矩形直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE＝125°， 则∠DBC的度数为 ．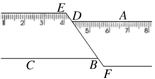
16. 如图，⊿ABC中，∠A = 30°，∠B = 70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F，则∠CDF =°
17. 如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内时，∠A与∠1＋∠2之间有始终不变的关系是.
18. 如果等式（2x+1）x-1=1，则x=.三、解答题
-
19. 计算：(1)、 ；(2)、3a3×2a6-3a12¸a3.(3)、（m－2n）（m+2n）(4)、（x+2y-3）（x-2y+3）20. 把下列各式分解因式：(1)、4a2﹣16(2)、（y-1）2-10（y-1）+25(3)、（x+2）（x+4）+121. 先化简，再求值：（2a-1）2+6a（a+1）-（3a+2）（3a-2），其中a2+2a-2020=0.22. 如图，在每个小正方形边长为1的方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′.根据下列条件，利用格点和三角尺画图：
(1)、①补全△A′B′C′；②请在AC边上找一点D，使得线段BD平分△ABC的面积，在图上作出线段BD；
③利用格点在图中画出AC边上的高线BE；
(2)、求△ABD的面积.23. 如图，∠1=70°，∠2=110°，∠C=∠D，试探索∠A与∠F有怎样的数量关系，并说明理由.
24. 已知：如图所示，在△ABC中，D是BC边上一点，∠1=∠B，∠2=∠C，∠BAC=75°，求∠DAC的度数.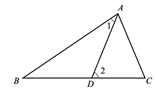
25. 如图
(1)、如图是用4个全等的长方形拼成的一个“回形”正方形，将图中阴影部分面积用2种方法表示可得一个等式，这个等式为；(2)、若（3x－2y）2＝5，（3x＋2y）2＝8，求xy的值.26. 如图1，直线m与直线n垂直相交于O，点A在直线m上运动，点B在直线n上运动，AC、BC分别是∠BAO和∠ABO的角平分线.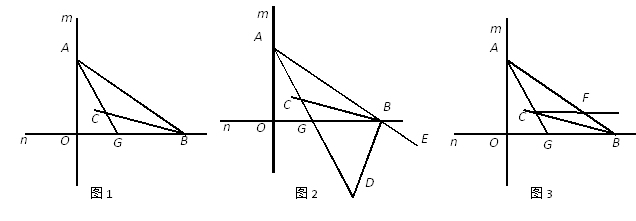
(1)、求∠ACB的大小；(2)、如图2，若BD是△AOB的外角∠OBE的角平分线，BD与AC相交于点D，点A、B在运动的过程中，∠ADB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；(3)、如图3，过C作直线与AB交于F，且满足∠AGO－∠BCF=45°，求证：CF∥OB.