江苏省无锡市滨湖区2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-06-05 类型:期中考试
一、选择题
-
1. 下列汽车商标图案中,可以由一个“基本图案”通过连续平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式运算正确的是( )A、 B、 C、 D、3. 下列各式中,计算结果是 的是( )A、 B、 C、 D、4. 若 ,则 等于( )A、7 B、4 C、2 D、65. 有4根小木棒,长度分别为2cm、3cm、4cm、5cm,任意取3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为( )A、1个 B、2个 C、3个 D、4个6. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、
2. 下列各式运算正确的是( )A、 B、 C、 D、3. 下列各式中,计算结果是 的是( )A、 B、 C、 D、4. 若 ,则 等于( )A、7 B、4 C、2 D、65. 有4根小木棒,长度分别为2cm、3cm、4cm、5cm,任意取3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为( )A、1个 B、2个 C、3个 D、4个6. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、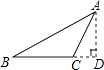 B、
B、 C、
C、 D、
D、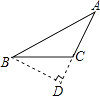 7. 若多项式 是一个完全平方式,则 的值是( )A、2 B、4 C、 D、8. 如图,把长方形纸片 沿 折叠,点 、 分别落在 、 处. 与 交于点 ,若 ,则 的度数为( )
7. 若多项式 是一个完全平方式,则 的值是( )A、2 B、4 C、 D、8. 如图,把长方形纸片 沿 折叠,点 、 分别落在 、 处. 与 交于点 ,若 ,则 的度数为( )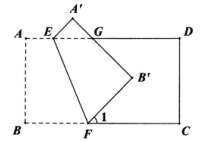 A、110° B、115° C、120° D、130°9. 有一张边长为 的正方形桌面,因实际需要,需将正方形边长增加 ,木工师傅设计了如图际所示的方案,该方案能验证的等式是( )
A、110° B、115° C、120° D、130°9. 有一张边长为 的正方形桌面,因实际需要,需将正方形边长增加 ,木工师傅设计了如图际所示的方案,该方案能验证的等式是( )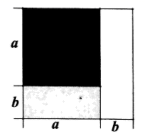 A、 B、 C、 D、10. 任何一个正整数 都可以进行这样的分解: ( 、 是正整数,且 ),如果 在 的所有这种分解中两因数之差的绝对值最小,我们就称 是 的最佳分解,并规定: .例如18可以分解成 , , 这三种,这时就有 ,给出下列关于 的说法:
A、 B、 C、 D、10. 任何一个正整数 都可以进行这样的分解: ( 、 是正整数,且 ),如果 在 的所有这种分解中两因数之差的绝对值最小,我们就称 是 的最佳分解,并规定: .例如18可以分解成 , , 这三种,这时就有 ,给出下列关于 的说法:① ;② ;③ ;④若 是一个完全平方数,则 ,其中正确说法的个数是( )
A、4 B、3 C、2 D、1二、填空题
-
11. 甲型 流感病毒的直径大约是0.000000081米,用科学记数法可表示为米.12. 一个多边形的内角和是 1440°,则这个多边形是边形.13. 计算: .14. 若 , ,则 .15. 如图,将周长为20个单位的 沿边 向右平移4个单位得到 ,则四边形 的周长为.
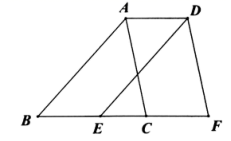 16. 如果 , ,那么 .17. 若 ,则 .18. 如图, 、 是 的两条高,它们相交于点 ,已知 的度数为 , 的度数为 ,则 的度数是.
16. 如果 , ,那么 .17. 若 ,则 .18. 如图, 、 是 的两条高,它们相交于点 ,已知 的度数为 , 的度数为 ,则 的度数是.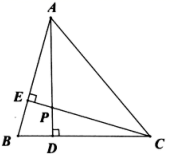
三、解答题
-
19. 计算:(1)、 ;(2)、 ;(3)、 ;(4)、 .20. 先化简,再求值: ,其中 , .21. 春天到了,为了试验某种杀菌剂的效果,实验室进行了实验,研究发现房间空气中每立方米含 个病菌,已知1毫升杀菌剂可以杀死 个这种病菌,问要将长5米、宽4米、高3米的房间内的病菌全部杀死,需多少毫升杀菌剂?22. 如图,在 中,点D、E分别在AB、BC上,且 , .问AF与BC有怎样的位置关系?为什么?
 23. 如图,在每个小正方形边长为1的方格纸中, 的顶点都在方格纸格点上.
23. 如图,在每个小正方形边长为1的方格纸中, 的顶点都在方格纸格点上.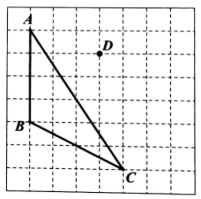 (1)、①将 经过平移后得到 ,图中标出了点A的对应点D,补全 ;
(1)、①将 经过平移后得到 ,图中标出了点A的对应点D,补全 ;②在图中画出 的中线BG和高CH;
(2)、在(1)条件下,AD与CF的关系是.24. 阅读理解:若 ,求 、 的值.解:∵ ,
∴ ,
∴ ,
∴ 且 ,
∴ .
方法应用:
(1)、 ,则 , ;(2)、已知 , ,求 的值.25. 如图, , 平分 ,点A、B、C分别是射线OM、OE、ON上的动点(点A、B、C不与点 重合),且 ,连接AC交射线OE于点D. (1)、求 的度数;(2)、当 中有两个相等的角时,求 的度数.26. 如图,直线 和直线 互相垂直,垂足为 ,直线 于点B,E是线段AB上一定点,D为线段OB上的一动点(点D不与点O、B重合), 直 于点 ,连接AC.
(1)、求 的度数;(2)、当 中有两个相等的角时,求 的度数.26. 如图,直线 和直线 互相垂直,垂足为 ,直线 于点B,E是线段AB上一定点,D为线段OB上的一动点(点D不与点O、B重合), 直 于点 ,连接AC.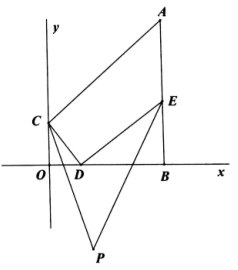 (1)、当 ,则 °;(2)、当 时,请判断CD与AC的位置关系,并说明理由;(3)、若 、 的角平分线的交点为P,当点D在线段 上运动时,问 的大小是否会发生变化?若不变,求出 的大小,并说明理由;若变化,求其变化范围.
(1)、当 ,则 °;(2)、当 时,请判断CD与AC的位置关系,并说明理由;(3)、若 、 的角平分线的交点为P,当点D在线段 上运动时,问 的大小是否会发生变化?若不变,求出 的大小,并说明理由;若变化,求其变化范围.