江苏省泰州市高港区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-06-05 类型：期中考试

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{3} \cdot a^{4} = a^{12}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $a \div a^{- 2} = a^{3} (a \neq 0)$

查看试题解析
2. 2020年新冠肺炎席卷全球，KN95口罩紧缺，因为它既能有效防范病毒传播又能有效过滤空气中的PM2.5.PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物.2.5微米等于0.0000025米，把0.0000025用科学记数法表示为（）

A、 0.25×10^–5 B、2.5×10^–7 C、2.5×10^–6 D、25×10^–7

查看试题解析
3. 下列等式从左到右的变形，属于因式分解的是（）

A、a（x－y）＝ax－ay B、x²－1＝（x+1）（x－1） C、（x+1）（x+3）＝x²+4x+3 D、x²+2x+1＝x（x+2）+1

查看试题解析
4. 已知∠1与∠2是内错角，则（）

A、∠1=∠2 B、∠1＞∠2 C、∠1＜∠2 D、以上都有可能

查看试题解析
5. 如果 $a = {(- 99)}^{0} ，$ $b = {(- 0.1)}^{- 1}$ ， $c = {(- \frac{5}{3})}^{- 2}$ ，那么 $a ， b ， c$ 三数的大小为（）

A、 $a > b > c$ B、 $a > c > b$ C、 $c > a > b$ D、 $c > b > a$

查看试题解析
6. 为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法（）

A、4 B、3 C、2 D、1

查看试题解析
7. 计算：(-m-n)(m-n)=（）

查看试题解析
8. 若多项式x²＋kx＋9是一个完全平方式，则k的值等于.

查看试题解析
9. 如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是．

查看试题解析

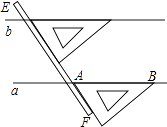
二、填空题

10. 已知 $2 x + y + 1 = 0$ ，则 $5^{2 x} \cdot 5^{y}$ =.

查看试题解析
11. 已知x﹣ $\frac{1}{x}$ ＝6，求x²+ $\frac{1}{x^{2}}$ 的值为.

查看试题解析
12. 若(x+a)(x-3)的结果中不含关于字母x的一次项，则a=.

查看试题解析
13. 如果一张长方形的纸条，如图所示折叠，那么∠α等于.

查看试题解析
14. 已知 $P = m^{2} - m$ ， $Q = m - 1$ （ $m$ 为任意实数），则 $P$ $Q$ .（用不等号连接）

查看试题解析
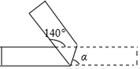15. 若代数式 $x^{2} - 3 x + 2$ 可以表示为 ${(x + 1)}^{2} + a (x + 1) + b$ 的形式，则a-b的值是.

查看试题解析
16. 大正方形的边长为4厘米，小正方形的边长为2厘米，起始状态如图所示，现把小正方形以1厘米/秒的速度向右沿直线平移，同时大正方形以1厘米/秒的速度向左沿直线平移，设平移的时间为t秒，两个正方形重叠部分的面积为S平方厘米.当S＝2时，平移的时间为秒.

查看试题解析

三、解答题

17. 计算或化简

(1)、 ${(\frac{1}{2})}^{- 3} - 2020^{0} - | - 5 |$ ；

(2)、 $a^{5} \cdot {(a^{4})}^{2} \div {(- a^{2})}^{3}$ ；

(3)、 ${(\frac{1}{2})}^{2019} \times {(- 2)}^{2020}$ .

查看试题解析
18. 因式分解

(1)、-2x²+8；

(2)、 $x^{3} - 2 x^{2} y + x y^{2}$ ；

(3)、 ${(x^{2} + 4)}^{2} - 16 x^{2}$ .

查看试题解析
19. 解方程组

(1)、 ${\begin{array}{l} 2 x + 3 y = 13 \\ x - 2 y = - 4 \end{array}$

(2)、 ${\begin{matrix} 3 (x - 1) - 4 (y + 1) = - 1 \\ \frac{x}{2} + \frac{y}{3} = - 2 \end{matrix}$

查看试题解析
20. 先化简，再求值： $(2 m + 1) (2 m - 1) - {(m - 1)}^{2} + {(2 m)}^{3} \div (- 8 m)$ ，其中 $m^{2} + m - 2 = 0$

查看试题解析
21.

(1)、已知 $a^{m} = 2$ ， $a^{n} = 3$ ，求:
① $a^{m + n}$ 的值;

② $a^{3 m - 2 n}$ 的值;

(2)、已知 $2 \times 8^{x} \times 16 = 2^{23}$ ，求 $x$ 的值

查看试题解析
22. 如图， $∠ α$ 和 $∠ β$ 的度数满足方程组 ${\begin{array}{l} 3 ∠ α + ∠ β = 260 ° \\ ∠ β - ∠ α = 100 ° \end{array}$ ，且 $C D / / E F$ ， $A C ⊥ A E$ .

(1)、求证 $A B / / E F$ ；

(2)、求 $∠ C$ 的度数.

查看试题解析
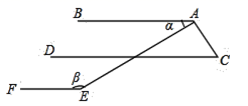23. 观察下列关于自然数的等式：
① $3^{2} - 4 \times 1^{2} = 5$ ；② $5^{2} - 4 \times 2^{2} = 9$ ；③ $7^{2} - 4 \times 3^{2} = 13$ ；…

根据上述规律解决下列问题：

(1)、请仿照①、②、③，直接写出第4个等式：；

(2)、请写出你猜想的第n个等式（用含n的式子表示），并证明该等式成立.

查看试题解析
24. 为了响应“足球进校园”的目标，某校计划为学校足球队购买一批足球，已知购买2个A品牌的足球和3个B品牌的足球共需380元；购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)、求A，B两种品牌的足球的单价.

(2)、该校打算通过“京东商城”网购20个A品牌的足球和3个B品牌的足球，“五一”期间商城打折促销，其中A品牌打八折，B品牌打九折，问：学校购买打折后的足球所花的费用比打折前节省了多少钱？

查看试题解析
25. 如图

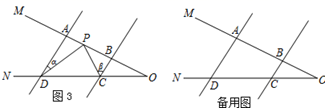(1)、问题情境：如图1，AB∥CD，∠PAB=135°，∠PCD=125°.求∠APC度数.小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可求得∠APC的度数.请写出具体求解过程.

(2)、问题迁移：如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系？请说明理由；

(3)、在(1)的条件下，如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合)，请你直接写出∠CPD、∠α、∠β间的数量关系.

查看试题解析
26. 数学活动课上，老师准备了若干个如图1的三种纸片， $A$ 种纸片是边长为 $a$ 的正方形， $B$ 种纸片是边长为 $b$ 的正方形， $C$ 种纸片是长为 $b$ ，宽为 $a$ 的长方形.并用 $A$ 种纸片一张， $B$ 种纸片一张， $C$ 种纸片两张拼成如图2的大正方形.

(1)、请用两种不同的方法求图2大正方形的面积：方法1：；方法2：；

(2)、观察图2，请你写出代数式： ${(a + b)}^{2} ， a^{2} + b^{2} ， a b$ 之间的等量关系；

(3)、根据（2）题中的等量关系，解决如下问题：
①已知： $a + b = 5 ， a^{2} + b^{2} = 13$ ，求 $a b$ 的值；

②已知 ${(2020 - a)}^{2} + {(a - 2019)}^{2} = 5$ ，求 $(2020 - a) (a - 2019)$ 的值；

③已知(a-2019)²+(a-2021)²=8，则求(a-2020)²的值.

查看试题解析