江苏省太仓市校际联合2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-06-05 类型:期中考试
一、选择题
-
1. 下列图形中,不能通过其中一个四边形平移得到的是( )A、
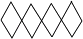 B、
B、 C、
C、 D、
D、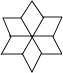 2. 计算 的结果是( )A、 B、 C、 D、3. 下列四个等式从左到右的变形是因式分解的是 ( )A、 B、 C、 D、4. 将一副三角板(含30°、45°的直角三角形)摆放成如图所示,图中∠1的度数是( )
2. 计算 的结果是( )A、 B、 C、 D、3. 下列四个等式从左到右的变形是因式分解的是 ( )A、 B、 C、 D、4. 将一副三角板(含30°、45°的直角三角形)摆放成如图所示,图中∠1的度数是( )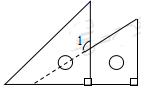 A、90° B、120° C、135° D、150°5. 等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )A、12 B、15 C、12或15 D、186. 将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )
A、90° B、120° C、135° D、150°5. 等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )A、12 B、15 C、12或15 D、186. 将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )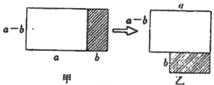 A、 B、 C、 D、7. 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
A、 B、 C、 D、7. 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )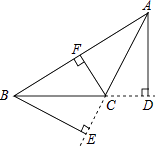 A、CF B、BE C、AD D、CD8. 若 , ,则 的值为( )A、12 B、20 C、32 D、2569. 在餐馆里,王伯伯买了5个菜,3个馒头,老板少收2元,只收50元,李太太买了11个菜,5个馒头,老板以售价的九折优惠,只收90元,若菜每个x元,馒头每个y元,则下列能表示题目中的数量关系的二元一次方程组是( )A、 B、 C、 D、10. 观察下列等式: , , , , , , ,试利用上述规律判断算式 结果的末位数字是( )A、0 B、1 C、3 D、7
A、CF B、BE C、AD D、CD8. 若 , ,则 的值为( )A、12 B、20 C、32 D、2569. 在餐馆里,王伯伯买了5个菜,3个馒头,老板少收2元,只收50元,李太太买了11个菜,5个馒头,老板以售价的九折优惠,只收90元,若菜每个x元,馒头每个y元,则下列能表示题目中的数量关系的二元一次方程组是( )A、 B、 C、 D、10. 观察下列等式: , , , , , , ,试利用上述规律判断算式 结果的末位数字是( )A、0 B、1 C、3 D、7二、填空题
-
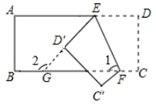
11. 计算:()2= .12. 我国开展的月球探测工程(即“嫦娥工程”)为人类和平使用月球作出了新的贡献.地球与月球之间的平均距离大约为384000km,384000用科学记数法可表示为.13. 若 ,则 .14. 如果关于 的方程 和 的解相同,那么m=.15. 关于 的方程组 的解是 ,则 的值是.16. 若a+b=4,a﹣b=1,则(a+1)2﹣(b﹣1)2的值为 .17. 如图,将长方形纸片 沿着 ,折叠后,点 分别落在点 D'、C' 的位置, 的延长线交 于点 .若 ,则 等于度.
 18. 如图,把 纸片沿 折叠,使点 落在四边形 的外部.已知 , ,则 的度数是度.
18. 如图,把 纸片沿 折叠,使点 落在四边形 的外部.已知 , ,则 的度数是度.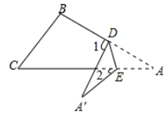
三、解答题
-
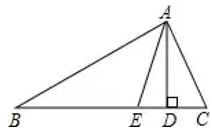
19. 计算(1)、 ;(2)、 .20. 分解因式(1)、 ;(2)、 .21. 先化简后求值: ,其中 , .22. 在抗击新型冠状肺炎期间,我市某企业向湖北武汉捐赠了价值26万元的甲、乙两种仪器共30套.已知甲种仪器每套8000元,乙种仪器每套10000元,问甲、乙两种仪器各捐赠了多少套?23. 如图,已知 中, 分别是 的高和角平分线.若 , ,求 的度数.
 24. 已知 ,且 ,求 的值.25. 已知: , .求下列代数式的的值.(1)、 ;(2)、 ;(3)、 .26. 已知关于 的方程组 ,(1)、请用 的代数式表示 ;(2)、若 互为相反数,求 的值.27. 如图,在 的 边的异侧作 ,并使 .点 在射线 上.
24. 已知 ,且 ,求 的值.25. 已知: , .求下列代数式的的值.(1)、 ;(2)、 ;(3)、 .26. 已知关于 的方程组 ,(1)、请用 的代数式表示 ;(2)、若 互为相反数,求 的值.27. 如图,在 的 边的异侧作 ,并使 .点 在射线 上.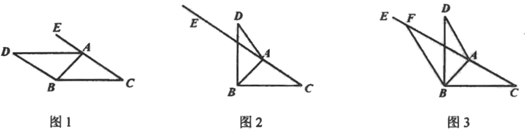 (1)、如图,若 ,求证: ;(2)、若 ,试解决下面两个问题:
(1)、如图,若 ,求证: ;(2)、若 ,试解决下面两个问题:①如图2, ,求 的度数;
②如图3,若 ,过点 作 交射线 于点 ,当 时,求 的度数.
28. 如图1,在 中, 平分 , 平分 .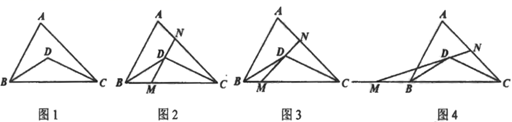 (1)、若 ,则 的度数为;(2)、若 ,直线 经过点 .
(1)、若 ,则 的度数为;(2)、若 ,直线 经过点 .①如图2,若 ,求 的度数(用含 的代数式表示);
②如图3,若 绕点 旋转,分别交线段 于点 ,试问在旋转过程中 的度数是否会发生改变?若不变,求出 的度数(用含 的代数式表示),若改变,请说明理由:
③如图4,继续旋转直线 ,与线段 交于点 ,与 的延长线交于点 ,请直接写出 与 的关系(用含 的代数式表示).