江苏省无锡市锡山区2020届九年级下学期数学期中考试试卷

试卷更新日期：2020-06-05 类型：期中考试

进入出卷网下载

一、让填空题

1. 2020年4月11日中国向蒙古国紧急援助490000只口罩，表达了中国人民愿同蒙古国携手抗疫、共克时艰的决心和信心.把490000用科学记数法表示为.

查看试题解析
2. 因式分解：x²-4y²= .

查看试题解析
3. 已知点M(m,n)与点N(－2,－3)关于x轴对称，则m＋n＝.

查看试题解析
4. 六边形的外角和等于°.

查看试题解析
5. 命题“四边相等的四边形是菱形”的逆命题是．

查看试题解析
6. 如图，一次函数y=kx+b的图像经过A、B两点，那么关于x的不等式kx+b>0的解集是.

查看试题解析
7. 如图，在△BDE中，∠BDE＝90°，BD＝4，点D的坐标是(6，0)，∠BDO＝15°，将△BDE旋转到△ABC的位置，点C在BD上，则旋转中心的坐标为.

查看试题解析
8. 在 $R t Δ A B C$ 中， $∠ C = 90^{\circ}$ ， $A D$ 平分 $∠ C A B$ ， $B E$ 平分 $∠ A B C$ ， $A D 、 B E$ 相交于点 $F$ ，且 $A F = 4 ， E F = \sqrt{2}$ ，则 $A C =$ .

查看试题解析

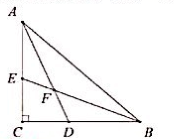
二、解答题

9. 计算：

(1)、 ${(\frac{1}{3})}^{0} + \sqrt{27} - | - 3 | + \tan 45^{°}$ ；

(2)、 $(x + 3) (x - 3) - {(x - 2)}^{2}$ .

查看试题解析
10.

(1)、解方程： $\frac{2 - x}{x - 3} = 1 - \frac{1}{3 - x}$ ；

(2)、解不等式组： ${\begin{array}{l} 2 x - 1 \leq 2 \\ \frac{x - 1}{4} < \frac{x}{3} \end{array}$

查看试题解析
11. 如图，已知点B、E、C、F在同一条直线上，AB=DE，∠A=∠D，AC∥DF．求证：BE=CF．

查看试题解析
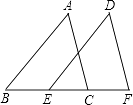12. 由于2020年新型冠状病毒的袭击，不得不推迟开学，但停课不停学，各地都开展了网课.某中学为了解学生上网课情况，开学后从全校七年级学生中随机抽取部分学生进行了数学科目的测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：合格；D级：不合格），并将测试记录绘成如下两幅完全不同的统计图，请根据统计图中的信息解答下列问题：

(1)、本次抽样测试的学生数是多少？

(2)、求图1中A级扇形的圆心角∠α的度数，并把图2中的条形统计图补充完成；

(3)、该中学七年级共有1200名学生，如果全部参加这次数学科目测试，请估计不合格的人数.

查看试题解析
13. 为落实“垃圾分类”，环保部门要求垃圾要按A，B，C，D四类分别装袋、投放，其中A类指废电池、过期药品等有害垃圾；B类指剩余食品等厨余垃圾；C类指塑料、废纸等可回收物；D类指其他垃圾.小明投放了一袋垃圾，小亮投放了两袋不同类垃圾.

(1)、直接写出小明投放的垃圾恰好是A类的概率是；

(2)、如果小明投放的垃圾是A类，请用画树状图或列表的方法求小亮投放的垃圾恰有一袋与小明投放的垃圾是同类的概率.

查看试题解析
14. 数学中我们学习了尺规作图，小明发现有些作图只用一种工具就可以完成，你能解决下列问题吗？

(1)、请只用无刻度的直尺完成下列作图，不写画法，保留画图痕迹（用虚线表示画图过程，实线表示画图结果）在图1中，过点A画一条直线把正五边形ABCDE分成面积相等的两部分；

(2)、已知直线l及l外一点A（按下列要求作图，不写画法，保留画图痕迹）.
①在图2中，只用圆规在直线l上画出两点B、C，使得点A、B、C是一个等腰三角形的三个顶点；

②在图3中，只用圆规在直线l外画出一点P，使得点A、P所在直线与直线l平行.

查看试题解析
15. 如图，AC是⊙O的直径，AB是⊙O的一条弦，AP是⊙O的切线，作BM＝AB并与AP交于点M，延长MB交AC于点E，交⊙O于点D，连接AD.

(1)、求证：AB＝BE；

(2)、若⊙O的半径R＝2.5，MB＝3，求AD的长.

查看试题解析
16. 龙虾狂欢季再度开启，第 $18$ 届中国合肥龙虾节的主题是“让你知虾，也知稻”，稻田小龙虾养殖技术在合肥周边的乡镇大力推广，已知每千克小龙虾养殖成本为 $6$ 元，在整个销售旺季的 $80$ 天里，销售单价 $p$ 元/千克，与时间 $t$ （天）之间的函数关系式为： $P = {\begin{array}{l} \frac{1}{4} t + 16 (1 \leq t \leq 40 ， t 为整数) \\ - \frac{1}{2} t + 46 (41 \leq t \leq 80 ， t 为整数) \end{array}$ ，日销售量 $y$ （千克）与时间第 $t$ （天）之间的函数关系如图所示：

(1)、求日销售量 $y$ 与时间 $t$ 的函数关系式？

(2)、哪一天的日销售利润最大？最大利润是多少？

(3)、在实际销售的前 $40$ 天中，该养殖户决定销售 $1$ 千克小龙虾，就捐赠 $m (m < 7)$ 元给村里的特困户，在这前 $40$ 天中，每天扣除捐赠后的日销售利润随时间 $t$ 的增大而增大，求 $m$ 的取值范围.

查看试题解析
17. 在 $Δ A B C$ ， $C A = C B$ ， $∠ A C B = α$ .点P是平面内不与点A，C重合的任意一点.连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP.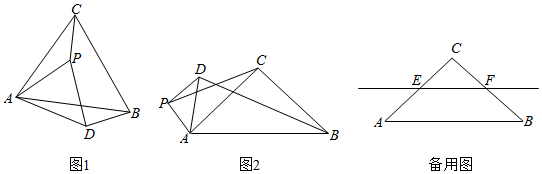

(1)、观察猜想
如图1，当 $α = 60^{°}$ 时， $\frac{B D}{C P}$ 的值是，直线BD与直线CP相交所成的较小角的度数是.

(2)、类比探究
如图2，当 $α = 90^{°}$ 时，请写出 $\frac{B D}{C P}$ 的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由.

(3)、解决问题
当 $α = 90^{°}$ 时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时 $\frac{A D}{C P}$ 的值.

查看试题解析
18. 如图1，在平面直角坐标系中，抛物线y＝ax²－2ax＋3与x轴交于点A，B（点A在点B的左侧），交y轴于点C，点A的坐标为(－1，0)，点D为抛物线的顶点，对称轴与x轴交于点E.

(1)、填空：a＝，点B的坐标是；

(2)、连结BD，点M是线段BD上一动点（点M不与端点B，D重合），过点M作MN⊥BD，交抛物线于点N（点N在对称轴的右侧），过点N作NH⊥x轴，垂足为H，交BD于点F，点P是线段OC上一动点，当△MNF的周长取得最大值时，求FP＋ $\frac{1}{2}$ PC的最小值；

(3)、在（2）中，当△MNF的周长取得最大值时，FP＋ $\frac{1}{2}$ PC取得最小值时，如图2，把点P向下平移 $\frac{2 \sqrt{3}}{3}$ 个单位得到点Q，连结AQ，把△AOQ绕点O顺时针旋转一定的角度α（0°＜α＜360°），得到△A′OQ′，其中边A′Q′交坐标轴于点G.在旋转过程中，是否存在一点G，使得GQ′＝OG？若存在，请直接写出所有满足条件的点Q′的坐标；若不存在，请说明理由.

查看试题解析